解析 に関する126記事をまとめました。くわしくは各リンク先を見てください。
リーマンのゼータ関数
s>1
なる実数に対して,ゼータ関数
ζ(s)
は以下のように定義される:
ζ(s)=n=1∑∞ns1=1s1+2s1+3s1+⋯
→ゼータ関数の定義と基本的な話
任意の実数
a,b(a<b)
に対して,
→有理数と無理数の稠密性
BSD予想 (バーチ・スウィンナートン=ダイアー予想)
楕円曲線 E の階数は,E の L 関数 L(s,E) の s=1 における零点の位数に等しい。
→BSD予想の主張の解説
→円周率が無理数であることの証明
楕円曲線
(実数上の)楕円曲線とは,
y2=x3+ax+b
により表される曲線である。ただし,x3+ax+b=0 は重解を持たないとする。
→楕円曲線~フェルマーの最終定理・BSD予想・合同数問題と合わせて
オイラーの公式
任意の実数 θ に対して,
eiθ=cosθ+isinθ
→オイラーの公式と複素指数関数
→関数の連続性と一様連続性
フレネル積分
∫−∞∞sinx2dx=2π
∫−∞∞cosx2dx=2π
→フレネル積分(sin x^2の積分)
多変数のガウス積分
∫exp(−21x⊤Ax+b⊤x)dx=detA(2π)nexp(21b⊤A−1b)
→多変数のガウス積分
ガンマ関数の定義(正の実数の場合)
正の実数 x に対して,
Γ(x)=∫0∞tx−1e−tdt
を返す関数 Γ(x) をガンマ関数と呼ぶ。
→ガンマ関数(階乗の一般化)の定義と性質
複素数の指数関数
任意の複素数
z=a+bi
に対して,ネイピア数
e
を底とする指数関数は以下を満たす:
ez=ea(cosb+isinb)
→複素数の対数関数とiのi乗の主値が実数であること
ディリクレ関数
実数全体で定義され,有理数のときに
1,無理数のときに
0
を取る関数をディリクレ関数と言う。
f(x)={10(x∈Q)(otherwise)
→ディリクレ関数の定義と有名な3つの性質
テイラーの定理
閉区間 [a,x] で n
回微分可能な関数 f について,
f(x)=k=0∑n−1f(k)(a)k!(x−a)k+f(n)(c)n!(x−a)n
を満たす
c(a<c<x) が存在する。

→テイラーの定理とテイラー展開~例と証明
変数分離形

変数分離形の微分方程式とは,
dxdy=p(x)q(y)
のように,dxdy=(x
の関数)×(y
の関数)と表せる微分方程式のこと。
→変数分離形の微分方程式の解法と例題
一般化二項定理
∣x∣<1
なる複素数
x
と,任意の複素数
α
に対して
(1+x)α=1+αx+2!α(α−1)x2+⋯
が成立する。
→一般化二項定理とルートなどの近似
関数列の収束には各点収束と一様収束という2つの概念があり,一様収束の方が強い。大雑把な意味は,
- 各点収束 → 各点でそれぞれ収束
- 一様収束 →すべての点が一気に収束
→各点収束と一様収束の違いと具体例
定理
i=1∑∞ai が絶対収束すれば,もとの級数自身も収束する。
→絶対収束と条件収束の意味と具体例
時刻
t
における放射性炭素C14の個数を
N(t)
とすると,dtdN(t)=−λN(t) が成立する(λ
は崩壊のスピードを表す定数)。
→放射性炭素年代測定法の原理と微分方程式
要素が実数である集合
A
に対して
-
maxA:A の最大値,maximum(英語),マックス(読み方の例)
-
minA:A の最小値,minimum,ミン
-
supA:A の上限,supremum,スープ
-
infA:A の下限,infimum,インフ
→sup(上限)とinf(下限)の意味,max・minとの違い
一変数関数 f(x) が以下を満たすとき,C1 級関数であるという。
一般に n 回微分可能で n 次導関数が連続である関数を Cn 級関数という。
任意の正の整数 n について Cn 級である関数を C∞ 級関数という。
→C1級関数,Cn級関数などの意味と具体例
最大値の定理
有界閉区間上の連続関数は最大値を持つ。
→ロルの定理,平均値の定理とその証明
フーリエ級数展開
f(x)
が周期
T
の「まともな」関数なら
f(x)=2a0+n=1∑∞(ancosT2πnx+bnsinT2πnx)
ただし,
an=T2∫0Tf(x)cosT2πnxdx
bn=T2∫0Tf(x)sinT2πnxdx
→フーリエ級数展開の公式と意味
定理:多変数関数の極値判定法
多変数関数 f(x1,⋯,xn) が点 p=(p1,⋯,pn) において,fx1(p)=⋯=fxn(p)=0(偏微分がすべて 0)を満たし,さらに,
- p での f のヘッセ行列が正定値である場合,極小値をとる。
- p での f のヘッセ行列が負定値である場合,極大値をとる。
→多変数関数の極値判定とヘッセ行列
フーリエ級数展開には
実三角関数 sinnx,cosnx で展開する表現と
複素指数関数 einx で展開する表現がある。
→複素数型のフーリエ級数展開とその導出
実用上多くの場合,偏微分の順序交換が可能。
つまり,fxy=fyx
→偏微分の順序交換の十分条件とその証明
二変数関数
f(x,y)
が
Cn
級なら,多くの場合,
f(a+h,b+k)≒t=0∑nt!1(h∂x∂+k∂y∂)tf(a,b)
と表される。
→二変数関数のテイラー展開の意味と具体例
- ヤコビ行列とは,多変数関数の偏微分係数を並べた行列。「微分係数」の多変数バージョン。
- ヤコビアンとは,ヤコビ行列の行列式。「拡大率」を表す。
→ヤコビ行列,ヤコビアンの定義と極座標の例
線形同次微分方程式について,y1 が解ならその定数倍 cy1 も解。 y1,y2 が解ならその和 y1+y2 も解。
→微分方程式の階数,線形性などの意味と具体例
微小領域の体積
r0≤r≤r0+Δr,θ0≤θ≤θ0+Δθ,ϕ0≤ϕ≤ϕ0+Δϕ
の部分の体積は,Δr,Δθ,Δϕ
が十分小さい(0
に近い)とき,
r02sinθ0ΔrΔθΔϕ
に近づく。
→三次元極座標についての基本的な知識
→勾配ベクトルの意味と例題
Lpノルムの定義
n
次元ベクトル
x=(x1,x2,⋯,xn)
および
1≦p<∞
なる
p
に対して
p∣x1∣p+∣x2∣p+⋯+∣xn∣p
を
x
の
Lp
ノルムと言い,∥x∥p
と書く。
→ノルムの意味とL1,L2,L∞ノルム
直交多項式の定義
どの2つを取っても互いに直交するような多項式の集合を直交多項式系と呼ぶ。
→直交多項式の意味と4つの有名な例
連鎖律(チェインルール)
(x,y)
から
(u,v)
が定まり,(u,v)
から
f
が定まるとき
∂x∂f=∂u∂f∂x∂u+∂v∂f∂x∂v∂y∂f=∂u∂f∂y∂u+∂v∂f∂y∂v
となる。
→連鎖律(チェインルール)~多変数関数の合成関数の微分
複素関数の微分可能性についての定理
z=x+iy(x,y は実数)とする。次の2条件は同値である。
-
f(z)=u(x,y)+iv(x,y) が複素関数の意味で微分可能(正則関数)
-
u(x,y),v(x,y) が(2変数実関数の意味で)全微分可能であり,コーシーリーマンの関係式を満たす。
(ただし,u,v は実数)
→コーシーリーマンの関係式と微分可能性・正則関数
この記事では,
∫0π∫0Rr4sinθdrdθ
のような重積分の計算方法を,例題を通じてわかりやすく解説します。
→重積分の計算方法と例題3問
定理
べき級数
n=0∑∞anzn
に対して,以下の1,2を両方満たす
ρ
(ただし
0≤ρ≤∞)が存在する:
- ∣z∣<ρ
ならこのべき級数は収束
- ∣z∣>ρ
ならこのべき級数は発散
→収束半径の意味と求め方
関数の極限の定義
任意の正の実数 ε に対して,ある正の実数 δ が存在して,0<∣x−a∣<δ なら ∣f(x)−A∣<ε
が成立するとき,x→alimf(x)=A とする。
→イプシロンデルタ論法とイプシロンエヌ論法
関数
y=f(x)
が2点
(x1,y1),(x2,y2)
を通ることがわかっているとする。このとき,関数
f(x)
を,2点を通る線分:
y=y1+x2−x1y2−y1(x−x1)
で近似する手法を線形補間と言う。
→線形補間の計算式と近似誤差
ガウスの発散定理の大雑把なイメージ
閉曲面 S を貫く水の総量は,その内部 V から湧き出したり,吸い込まれたりする量に等しい。
→ガウスの発散定理・ストークスの定理の証明
例題1
dtdx−3x=et+1
の一般解を求めよ。
→微分方程式の解法(同次形・線形微分方程式)
リッカチの微分方程式
dtdx=f(t)x2+g(t)x+h(t)
という形の微分方程式をリッカチ(Riccati)の微分方程式と言う。ただし f(t),g(t),h(t) は与えられた t の関数である。
→リッカチの微分方程式・ベルヌーイの微分方程式
フーリエ変換
可積分関数 f(x) のフーリエ変換(Fourier transform)f^(ξ) を
f^(ξ)=∫−∞∞f(x)e−ixξdx
と定める(可積分関数とは ∫−∞∞∣f(x)∣dx<∞ を満たす関数のこと)。
→フーリエ変換の意味と応用例
任意の(なめらかな)関数 f(x) に対して
∫−∞∞f(x)δ(x)dx=f(0)
を満たすような「仮想的な」関数 δ(x) を,ディラック(Dirac)のデルタ関数という。
→ディラックのデルタ関数
数列の上極限の定義
数列 {an} の上極限とは,n→∞lim(k≥nsupak) のこと。
数列 {an} の上極限を n→∞limsupan または n→∞liman と書く。
→limsup、liminfの意味(数列・集合の上極限・下極限)
前進オイラー法
xn+1=xn+hf(xn,t0+nh)
という漸化式と x0 に基づいて,x1,x2,… と順々に計算していく方法。
→オイラー法をわかりやすく解説
コーシーの積分定理
f を単連結な(つながっていて穴がない)領域 D 内で正則な複素関数とする。C は D 内の単純閉曲線(自分自身と交わらない閉じた曲線)とする。 このとき
∮Cf(z)dz=0
である。
→コーシーの積分定理と積分経路の変形
コーシーの積分公式(コーシーの積分表示)
- D を単純閉曲線(自分と交わらない閉じた曲線)で囲まれた領域とする。
- f を領域 D=D∪∂D で正則な関数とする。
このとき D の内部の任意の点 z で
f(z)=2πi1∮∂Dζ−zf(ζ)dζ
となる(線積分の向きは反時計回り,より厳密には領域の内側から見て左周りに定める)。
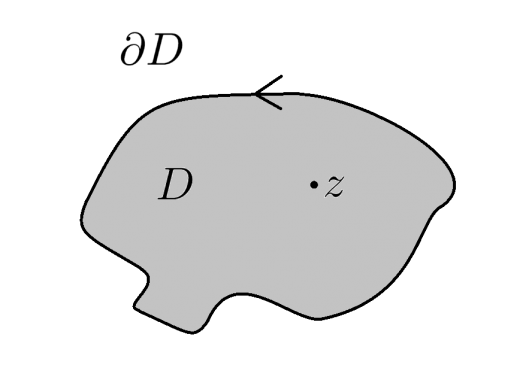
→コーシーの積分公式とその応用~グルサの定理・モレラの定理
ローラン展開(Laurent展開)
0<∣z−a∣<R で正則(微分可能)な複素関数 f(z) は,以下のようにべき級数展開できる。
f(z)=n=−∞∑∞an(z−a)n
ただし,各係数 an は
an=2πi1∮∣z−a∣=r(z−a)n+1f(z)dz
で計算できる (r は 0<r<R を満たす実数ならなんでもよい)。
→ローラン展開の意味・計算方法・特異点の分類
複素積分には非常に豊かな世界が広がっており,留数定理やコーシーの積分公式などの多種多様な定理・公式があります。
複素数の世界で積分をし,それを実数の世界に「もちこむ」ことで興味深い積分が計算できることもあります。例えばフレネル積分は sin(x2) の積分で,実の範囲だけでは計算ができません。
この記事では複素積分の導入を行います。例題も用意しています。複素解析への第一歩を踏み出しましょう。
→複素積分の導入~複素線積分とその性質
グリーンの定理
(単純)閉曲線 C と,C で囲まれた領域 D を考える。D 上で C1 級の任意の関数 P(x,y),Q(x,y) に対して以下が成り立つ。
∮C(P(x,y)dx+Q(x,y)dy)=∬D(∂x∂Q−∂y∂P)dxdy
→グリーンの定理
留数定理
- 単連結な領域 D 内に,区分的になめらかな単純閉曲線 C がある
- f(z) は C で囲まれた領域で有限個の点 {a1,a2⋯,an} を除いて正則
このとき,
2πi1∮Cf(z)dz=i=1∑nRes(f,ai)
である。ただし,Res(f,ai) は f(z) の z=ai での留数とする。
→留数定理
Liouville の定理(リュウビル・リウビルの定理)
複素平面 C 全体で正則な関数を整関数という。有界な整関数は定数関数のみである。
→リュウビルの定理と代数学の基本定理
問題
次の積分を求めよ。
- ∫0∞x21(x2+1)dx
- ∫0∞xa(x+1)dx(0<a<1)
- ∫0∞x2+4logxdx
→留数定理による対数・無理関数の積分
積分と極限の交換
∫abn→∞limfn(x)dx=n→∞lim∫abfn(x)dx
という式について,
- fn(x) が一様収束するなら成立する(十分条件)
- ただし,一般には成立しない
- 一様収束しなくても成立することがある(単調収束・一様有界など他の十分条件がある)
→積分と極限(無限和)の交換
リーマン球面
リーマン球面とは,複素平面 C に無限遠点 ∞ を追加したものである。リーマン球面を
C^,C
などと書く。
→リーマン球面と無限遠点
問題
次の積分を求めよ。
- ∫02π2+costdt
- ∫02π1−2acosθ+a2cos2θdθ(∣a∣<1)
- ∫0∞xsinxdx
- ∫−∞∞sinx2dx
- ∫0∞e−x2cos(ax)dx(a>0)
→留数定理を用いた三角関数の積分
問題
次の積分を求めよ。
- ∫−∞∞x2+1dx
- p.v.∫−∞∞x4−1dx
- ∫0∞x3+1dx
なお p.v.∫ は主値積分を意味する。(補足を参照)
→留数定理を用いた有理関数の積分
リーマンの可除特異点定理
f は,a を孤立特異点として持ち,Δ(a,R)\{a}={z∣0<∣z−a∣<R} 上で正則かつ有界な関数とする。このとき,a は除去可能特異点である。すなわち,f(a) を適切に追加で定めれば f は Δ(a,R) 上で正則にできる。
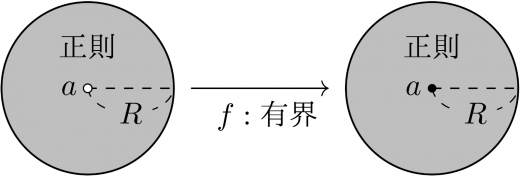
→リーマンの可除特異点定理
ベルヌーイ数の定義
ベルヌーイ数 Bn を
ex−1x=n=0∑∞n!Bnxn
と定める。
→ベルヌーイ数とゼータ関数
偏角の原理
D をなめらかな曲線に囲まれた有界な領域とする。
f を ∂D 上で極も零点も持たない D 上の有理型関数とする。
f の D 上の零点の(重複度を含めた)個数を N,極の(重複度を含めた)個数を P とする。このとき
2πi1∮∂Df(z)f′(z)dz=N−P
である。

※領域 D を囲うなめらかな曲線は,互いに交わらなければ複数個でも構いません。よって中心に穴が開いた領域にも偏角の原理を適応することができます。
→偏角の原理とルーシェの定理~方程式の解の個数について
最大値の定理・最小値の定理
有界閉区間 [a,b] 上の連続関数 f は,最大値・最小値を取る。
→最大値・最小値の定理
有界の定義
-
実数の集合 A に対して
A が有界であるとは,
「ある実数 m,M が存在して,任意の x∈A に対して m≦x≦M」となることを意味する。

-
A 上の関数 f が有界であるとは,f(A)={y∣∃x∈A,f(x)=y} が有界であることを意味する。
→有界とは何か~上界・上限と下界・下限
ボルツァーノ=ワイエルシュトラスの定理
実数列 {an} が有界であるとき,{an} は収束する部分列を持つ。
→ボルツァーノ=ワイエルシュトラスの定理
最大値の原理
-
有界な領域 D 上の正則関数 f(z) について,ある z0∈D で ∣f∣ が最大値を取るとき,f は定数関数である。
-
(1の対偶) D 上の定数ではない正則関数 f に対して,∣f∣ は D 内で最大値を取らない。
-
f が D=D∪∂D 上で連続であるとき,∣f∣ は ∂D 上で最大値を取る。
→最大値の原理とシュワルツの補題
一致の定理(特殊形)
f,g を領域 D 上の正則関数とする。
- f,g が D 内のある線分・なめらかな曲線上(D∩R など)で一致するとき,D 全体でも一致する。
- f,g が D 内の開集合
O 上で一致するとき,D 全体でも一致する。
※記事の後半でより一般的な主張を紹介します。
→一致の定理
距離空間
距離関数 d を持つ集合 X を 距離空間 といい (X,d) と書く。
→距離空間~位相空間論に向けた開集合・閉集合の一般化
重積分の変数変換
2変数 x,y を2変数 u,v に変換する。
このとき xy 平面上の領域 D が uv 平面上の領域 E に一対一に対応するとき,D 上の積分可能関数 f の重積分は次のように計算される。
∬Df(x,y)dxdy=∬Ef(x(u,v),y(u,v))∣detJ∣dudv
ただし ∣detJ∣ はヤコビ行列
J=⎝⎛∂u∂xdu∂y∂v∂x∂v∂y⎠⎞
の行列式(ヤコビアン)の絶対値である。
なお,n 変数のときも同様に計算される。
→重積分の変数変換とヤコビアン
バーゼル問題
n=1∑∞n21=6π2
→重積分を用いたバーゼル問題の美しい証明
ワイエルシュトラスのペー関数の定義
複素数 ω1,ω2 は ω2ω1∈/R を満たすとする。
格子 Λ={nω1+mω2:n,m∈Z}
に対するワイエルシュトラスのペー関数(楕円関数)を
℘(z)=z21+ω∈Λ\{0}∑((z−ω)21−ω21)
と定める。
→ワイエルシュトラスのペー関数
Lpノルムの定義
p を 1 以上の実数とする。X 上で定義された関数 f の Lp ノルムを
∥f∥p=(∫X∣f(x)∣pdx)p1
で定義する。
→Lp空間と様々な関数不等式~関数におけるヘルダーの不等式
積分と極限の交換
∫abn→∞limfn(x)dx=n→∞lim∫abfn(x)dx
は成立するか?
→ルベーグの収束定理
逐次積分できる条件
f が [a,b]×[c,d] 上で
- 可積分な連続関数
- 非負な連続関数
のいずれかを満たすなら,以下の式が成り立つ。
∫ab(∫cdf(x,y)dy)dx=∫[a,b]×[c,d]f(x,y)dxdy=∫cd(∫abf(x,y)dx)dy
つまり逐次積分と重積分は一致する(積分の順序を交換できる)。
- また,いずれかの順序での(絶対値の)積分値が有限の値になれば,積分の順序を入れ替えてよい。
- また,有界な閉領域上での連続関数の重積分の順序は入れ替えてよい。
→フビニの定理~重積分の計算について
三角関数の無限乗積展開
sinπz=πzn=1∏∞(1−n2z2)
→sin の無限乗積展開とワイエルシュトラスの因数分解定理
三角関数と部分分数分解
sin2πzπ2=n=−∞∑∞(z−n)21πcotπz=z1+n=1∑∞z2−n22z
ただし cotz=tanz1 である。
→三角関数の部分分数分解
ワイエルシュトラスのM判定法(優級数定理)
{fn} を集合 A 上の実数値関数列とする。
各 n に対して,任意の x∈A に対して ∣fn(x)∣<Mn となる定数 Mn があり,n=1∑∞Mn が収束するなら,n=1∑∞fn(x) は一様収束する。
→ ワイエルシュトラスのM判定法
ワイエルシュトラスのペー関数
複素数 ω1,ω2 は ω2ω1∈/R を満たすものとする。
格子 Λ={nω1+mω2:n,m∈Z}
に対するワイエルシュトラスのペー関数(楕円関数)を
℘(z)=z21+ω∈Λ\{0}∑((z−ω)21−ω21)
と定める。
→ワイエルシュトラスのペー関数~証明編
区間塊の性質
- ∅∈F
- A∈F であれば Ac∈F
- A,B∈F であれば A∪B∈F
→ルベーグ測度
可測関数とは
X 上の関数 f が可測であるとは,任意の a∈R∪{±∞} に対して
E(f>a)={x∈X∣f(x)>a}
が可測集合になることを指す。
→ルベーグ積分
関数 f(x) が x=a で連続であるとは
x→alimf(x)=f(a)
が成立することである。
また,定義域(考えている区間内)の任意の点
a で関数 f が連続のとき,f を連続関数と呼ぶ。
→位相空間論への第一歩~連続関数とは何なのか? いくつかの重要な定義
リーマン積分の定義
∣Δ∣→0limSΔ,ξ が,Δ や ξ によらず一定値 α に収束するとき,f(x) は [a,b] 上でリーマン積分可能と言う。この値 α を ∫abf(x)dx と書きリーマン積分と呼ぶ。
→リーマン積分
定理
定数係数の n 階斉次線形微分方程式
dtndnx+an−1dtn−1dn−1x+⋯+a1dtdx+a0x=0⋯(i)
の解の集合は,n 次元のベクトル空間になる。
→n階斉次線形微分方程式の解空間
リプシッツ条件について解説します。リプシッツ条件は,
- 大雑把に言うと「出力の変動が,入力の変動の定数倍でおさえられる」という条件です。詳しくは後述します。
- 微分方程式の初期値問題を考えるときに重要な条件です。
- リプシッツ条件を満たせば,微分方程式の解が一意に定まるので嬉しいです。
→リプシッツ条件と微分方程式の解の一意性
-
リーマン積分可能なら「ルベーグ積分の値=リーマン積分の値」
-
ルベーグ積分できるがリーマン積分できない場合がある
-
広義リーマン積分できるがルベーグ積分できない場合がある
→リーマン積分 VS ルベーグ積分
ディリクレ積分
∫0∞xsinxdx=2π
→フーリエ変換を用いた sinc 関数の積分
定理
フーリエ変換によって関数の畳み込みと積は入れ替わる。すなわち,
f∗g(ξ)=f^(ξ)g^(ξ)
となる。
→フーリエ変換と畳み込み
バーゼル問題
n=1∑∞n21=6π2
→重積分を用いたバーゼル問題の美しい証明 その2
コンパクトとは
コンパクトとは,ざっくり言うと「開集合で全体を覆うと,実は有限個で十分」となるような空間・集合のことです。

→位相空間論の基礎~コンパクト空間・点列コンパクト空間の意味
定理
k=0∑∞(3k+1)31−k=0∑∞(3k+2)31=8134π
→フーリエ変換を用いた無限級数の計算
イプシロン-エヌ論法
任意の
ε>0
に対して,ある
N
が存在して,n>N
なら
∣an−α∣<ε を満たすとき,数列 {an} は α に収束するといい,n→∞liman=α と書く。
→攻略! ε-N/ε-δ 論法~その1~
イプシロン-エヌ論法
任意の
ε>0
に対して,ある
N
が存在して,n>N
なら
∣an−α∣<ε を満たすとき,数列 {an} は α に収束するといい,n→∞liman=α と書く.
→攻略! ε-N/ε-δ 論法~その2~
∫x4+1dx=421{log(x2+2x+1)−log(x2−2x+1)+2arctan(2x+1)−2arctan(1−2x)}
→1/(x^4+1) の積分
問題(東大数学科院試 2021より)
p>21 に対して,次の値を求めよ。
Γ(2p1)1∫0∞xsin(xp)dx
ただし,正の実数 x に対して,Γ(x) は次式で与えられるものとする。
Γ(x)=∫0∞tx−1e−tdt
→三角関数と無理関数の合わさった積分(東大院2021より)
東大数学科院試 2021から抜粋
初期値が x(1)=a,dtdx(1)=b となる微分方程式
dt2d2x−t22x=t2
の解 x(t) を求めよ。
ただし t は正の実数とする。
→微分方程式の例題(東大院2021から)
ゼータ関数のオイラー積表示
ζ(s)=n=1∑∞ns1=p∏1−ps11
→ゼータ関数のオイラー積
イプシロン-エヌ論法
任意の
ε>0
に対して,ある
N
が存在して,n>N
なら
∣an−α∣<ε を満たすとき,数列 {an} は α に収束するといい,n→∞liman=α と書く.
→攻略! ε-N/ε-δ 論法~その3~
バーゼル問題
n=1∑∞n21=6π2
→留数定理を用いたバーゼル問題の美しい証明
定義(コーシー列)
数列 {an} がコーシー列であるとは,
n,m→∞lim∣an−am∣=0
であることを表す。
イプシロンデルタ論法の表現できちんと述べると,
任意の正の実数 ε に対し,ある正の整数 N があって,N より大きい任意の整数 n,m に対して
∣an−am∣<ε
となることを表す。
→コーシー列
位相空間とは,開集合・閉集合の構造が入った集合である。
→位相空間論への第一歩~開集合・閉集合について
逆写像定理(大雑把な説明)
Cr 級関数 f について,ある点 x0 で微分が 0 でない(ヤコビアンが 0 でない)なら,x0 の付近で逆関数 f−1 が存在して f−1 も Cr 級
→逆写像定理
陰関数定理(2次元版)
-
f を二変数の連続で微分可能な関数とする。
-
(p,q) を,f(p,q)=0,∂y∂f(p,q)=0 を満たす点とする。
このとき,(p,q) の近傍で定義される g(x) という関数があって f(x,g(x))=0 となる。つまり f(x,y)=0 という形の(性質のよい)関数は局所的に y=g(x) と表せる。
さらに g(x) の微分係数は dxdg=−fyfx となる。
→陰関数定理
多様体
多様体とは,局所的にユークリッド空間 Rn と微分同相になる空間である。
次の2つがポイントである。
- 球など曲がった図形をユークリッド空間と見なすことができる。
- 微分を考えることができる。
→多様体入門1~定義と簡単な例
定義
位相空間 X がハウスドルフ空間であるとは,任意の異なる2点 x,y∈X に対して,ある開近傍 x∈U,y∈V であり U∩V=∅ となるものが存在することである。

→位相空間論の基礎~ハウスドルフ空間
内積空間(計量ベクトル空間)
V を実ベクトル空間とする。x,y∈V に対して実数を定める関数
⟨x,y⟩:V×V→R が以下の1~4を満たすとき,⟨ , ⟩ を内積といい,V を内積空間(計量ベクトル空間)という。
- ⟨x,y⟩=⟨y,x⟩(エルミート性)
- ⟨x+ay,z⟩=⟨x,z⟩+a⟨y,z⟩(x,y,z∈V,a∈R)(線型性)
- ⟨x,x⟩≧0(正定値性)
- ⟨x,x⟩=0⇒x=0(非退化性)
→内積の入ったベクトル空間~内積空間(計量ベクトル空間)
ノルム空間
V は(複素)ベクトル空間とする。
∥ ∥:V→R が以下の1~4を満たすときに,∥ ∥ をノルムといい,V をノルム空間という。
- ∥x+y∥≦∥x∥+∥y∥(三角不等式)
- ∥cx∥=∣c∣∥x∥(x∈V,c∈C)
- ∥x∥≧0
- ∥x∥=0⟺x=0
→ノルム空間
定義
V を実ベクトル空間とする。
R
への線型写像
ϕ:V→R
を線型汎関数という。
線型汎関数の集合を
V∗={ϕ:V→R∣ϕ は線型写像}
と定める。
V∗ に和とスカラー倍を以下のように定めると,V∗ はベクトル空間になる。
- (ϕ+ψ)(x)=ϕ(x)+ψ(x)
- (cϕ)(x)=cϕ(x)
V∗ を V の双対ベクトル空間という。
※ 和の単位元は任意の x を 0 に送る線型写像である。
※ 複素ベクトル空間に対しても V から C への線型写像の集合を考えれば双対ベクトル空間が得られる。
→線型汎関数と双対ベクトル空間
近傍
X を位相空間とする。X の部分集合 V が 近傍 であるとは,x が V の内部にあること,つまり x∈V∘ であることである。
x の近傍全体の集合を x の近傍系 という。
→位相空間論への第一歩~近傍系について
定理
実ノルム空間 V について,中線定理
∥x+y∥2+∥x−y∥2=2(∥x∥2+∥y∥2)
が成立するとき,
⟨x,y⟩=41(∥x+y∥2−∥x−y∥2)
により内積が定まる。
またこうして得られた内積において
⟨x,x⟩=∥x∥
となる。
→ノルム空間はいつ内積空間になるのか?~証明
定理
ガンマ関数とゼータ関数は複素数全体に拡張(解析接続)される。
→ガンマ関数とゼータ関数の解析接続
ディガンマ関数
ディガンマ関数 ψ(z)とは,ガンマ関数の対数微分,すなわち
ψ(z)=dzdlogΓ(z)
のことである。
→ディガンマ関数
定理(一様収束するなら微分と極限は交換できる)
- {fn} は [a,b] 上の微分可能な関数列で f に収束
かつ
- {fn′} は [a,b] 上で一様収束
ならば,
n→∞limfn′(x)=f′(x)
となる。つまり,微分と極限が交換できる。
→微分と極限の交換
ガウスの無限積表示
z∈C に対して,ガンマ関数を
Γ(z)=n→∞limz(z+1)(z+2)⋯(z+n)nzn!
と定義することができる。
→ガンマ関数の無限積表示と相反公式
レルヒの公式
exp(∂s∂ζ(s,x) ∣∣s=0)=2πΓ(x)
ただし,ζ(s,x) はフルヴィッツのゼータ関数
ζ(s,x)=n=0∑∞(n+x)s1
である。(s>1,x>0)
→レルヒの公式
定義
Rn+1\{O} に次のように同値関係 ∼ を定める。
x=(x0,⋯,xn),y=(y0,⋯,yn) に対して
すべての i に対して xi=cyi (c=0)⟺x∼y
この同値関係による商
(Rn+1\{O})/∼
を射影空間 RPnと定義する。
→射影空間のハウスドルフ性・コンパクト性~商位相空間
陰関数定理によって定まる多様体
F:Rn→Rm を Cr 級関数とする。Z(F)={x∈Rn∣F(x)=0} とする。
任意の p∈Z(F) において
rank (JF)p=m
であれば
Z(F) は Cr 級可微分多様体である。
※ rank (JF)p=m という条件は
(JF)p:Rn→Rm が全射であると言い換えることができる。
→ 多様体入門2~陰関数定理から定まる多様体
定理
M,N を多様体とし,座標近傍系をそれぞれ {Uα,φα,Vα}α∈A,{Uβ′,φβ′,Vβ′}β∈B とする。
多様体の間の連続関数 f:M→N が Cr 級であるとは,
- 任意の α∈A,β∈B に対して
φβ′∘f∘φα−1:φα(Uα∩f−1(Uβ′))→Vβ′
(これは Rn の開集合から Rm の開集合への連続関数になる)が Cr 級である
ことをいう。
→多様体入門3~多様体の間の写像の可微分性
接ベクトル
接ベクトルとは,多様体の局所的な情報を持つベクトル空間である。
→多様体入門4~接ベクトル
定理
(複素)線型空間 g がリー環(リー代数)であるとは,次の3条件を満たす [,]:g×g→g が定義されることをいう。
- [,] は双線型である。つまり c∈C,x,y∈g に対して
[cx,y]=[x,cy]=c[x,y]
が成り立つ。
- 任意の x,y∈g に対して [x,y]=−[y,x] が成り立つ。(交代律)
- 任意の x,y,z∈g に対して
[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0
が成り立つ。(ヤコビ恒等式)
また,この括弧積をリー括弧積という。
→リー環入門~線型リー環・リー群との関係
この記事では基礎的なマクローリン展開の演習問題をまとめました。
→攻略! テイラー展開・マクローリン展開
定理:多変数関数の極値判定法
多変数関数 f(x1,⋯,xn) が点 p=(p1,⋯,pn) において,fx1(p)=⋯=fxn(p)=0(偏微分がすべて 0)を満たすとき,p を臨界点という。
-
臨界点 p での f のヘッセ行列の固有値がすべて正(正定値)である場合,極小値をとる。
-
臨界点 p での f のヘッセ行列の固有値がすべて負(負定値)である場合,極大値をとる。
-
臨界点 p での f のヘッセ行列の固有値が正の実数と負の実数から成る場合,鞍点になる。
→攻略! 二変数関数・多変数関数の極値判定
群構造を成す行列の集合を行列群という。代表的なものに GLn(C),SLn(C),O(n),U(n) がある。
→一般線型群・ユニタリ群・直交群
定義
レムニスケートの周長の長さと 2a の比をレムニスケート周率といって ϖ で表す。
ϖ=2∫011−r4dr
と表される。
→レムニスケート周率とレムニスケート関数
定義
関数 f(x) に対して
L[f](s)=∫0∞e−sxf(x)dx
という「s についての関数を返す変換」をラプラス変換という。
→ラプラス変換の定義と具体例・性質
定理
2変数関数 f(u,v) について,u=u(x,y),v=v(x,y) により x,y 変数に置換したとき,2階偏微分は次のようになる。
∂x2∂2f=∂u2∂2f(∂x∂u)2+2∂u∂v∂2f∂x∂u∂x∂v+∂v2∂2f(∂x∂v)2+∂u∂f∂x2∂2u+∂v∂f∂x2∂2v
∂x∂y∂2f=∂u2∂2f∂x∂u∂y∂u+∂u∂v∂2f∂y∂u∂x∂v+∂u∂v∂2f∂x∂u∂y∂v+∂v2∂2f∂x∂v∂y∂v+∂u∂f∂x∂y∂2u+∂v∂f∂x∂y∂2v
∂y2∂2f=∂u2∂2f(∂y∂u)2+2∂u∂v∂2f∂y∂u∂y∂v+∂v2∂2f(∂y∂v)2+∂u∂f∂y2∂2u+∂v∂f∂y2∂2v
なお,f,u,v はどれも C2 級関数としている。
→二階偏微分の連鎖律(chain rule)
定理
ベータ関数とは,p,q>0 に対して
B(p,q)=∫01xp−1(1−x)q−1dx
と定義される(広義)積分である。
→ベータ関数の基本的な性質~ガンマ関数との関係・広義積分の収束
f(x1,⋯,xn) を n 変数多項式とする。
このとき
{x=(x1,⋯,xn)∈Rn∣f(x)=0}
は Rn の閉集合である。
→位相空間論の基礎~多項式写像を用いた開・閉集合の証明
定理
-
位相空間 X が連結空間であるとは,次の条件を満たす開部分集合 X1,X2 が存在しないことをいう。
X1∪X2=X, X1∩X2=∅, X1,X2=∅
-
位相空間 X が弧状連結空間であるとは,任意の x0,x1∈X に対して,連続写像
c:[0,1]→X
であって,c(0)=x0,c(1)=x1 となるものが取れることをいう。この連続写像を道という。
→位相空間論の基礎~連結空間・弧状連結空間の意味













