距離空間～位相空間論に向けた開集合・閉集合の一般化

まずは，距離関数を理解しましょう。

距離関数は，集合 $X$ の2つの要素から「距離」を定める関数です。入力が $X$ の要素2つで，出力が非負の実数です。つまり $X \times X$ から $\mathbb{R}_{\geqq 0}$ への関数です。

上記1～3を距離の公理と言います。

まずは簡単な例です。

• 集合は $X=\mathbb{R}$（実数全体）
• 距離関数は $d(x,y)=|x-y|$

としましょう。つまり，任意の実数 $x,y$ に対して $|x-y|$ を「距離」と考えます。実際，関数 $d: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}_{\geqq 0}$ は以下の3つを満たすので，距離関数の例です。

1. $\mathbb{R}$ の任意の元 $x,y$ に対して，$d(x,y)=0 \Longleftrightarrow x=y$（非退化性）
2. $\mathbb{R}$ の任意の元 $x,y$ に対して，$d(x,y)=d(y,x)$（対称性）
3. $\mathbb{R}$ の任意の元 $x,y,z$ に対して，$d(x,y) + d(y,z) \geqq d(x,z)$（三角不等式）

実数上の絶対値による距離 $|x-y|$ 以外にも様々な距離空間を考えることができます。

ユークリッド距離

$\mathbb{R}^n$ の2元 $x = (x_1, x_2 , \cdots ,x_n)$，$y = (y_1, y_2 , \cdots , y_n)$ の距離を $$d(x,y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2}$$ と定めると，距離の公理を満たします。

$L^1$（マンハッタン距離）

平面上の2点 $\mathrm{P} (x_1,y_1)$，$\mathrm{Q} (x_2,y_2)$ に対して $$d(\mathrm{P} , \mathrm{Q}) = |x_1-x_2|+|y_1-y_2|$$ と定義すると $d$ は距離関数となります。

より一般に $\mathbb{R}^n$ の2元 $x = (x_1, x_2 , \cdots ,x_n)$，$y = (y_1, y_2 , \cdots , y_n)$ に対して $$d(x,y) = |x_1 - y_1| + |x_2 - y_2| + \cdots + |x_n - y_n|$$ と定義すると距離の公理を満たします。

→ L1距離（マンハッタン距離）の意味と性質

$L^p$ 空間

有限次元版

$\mathbb{R}^n$ の2元 $x = (x_1, x_2 , \cdots ,x_n)$，$y = (y_1, y_2 , \cdots , y_n)$ に対して $$d(x,y) = \sqrt[p]{(x_1 - y_1)^p + (x_2 - y_2)^p + \cdots + (x_n - y_n)^p}$$ と定義すると距離の公理を満たします。

関数空間

$I \subset \mathbb{R}$ 上の関数 $f$ が $$\left( \int_I |f|^p dx \right)^{\frac{1}{p}} < \infty$$ を満たすとき，$f$ を $p$ 乗可積分 といいます。$p$ 乗可積分となる関数の集合を $L^p$ と書きます。

$$||f||_p = \left( \int_I |f|^p dx \right)^{\frac{1}{p}}$$ と定義し， $$d_p (f,g) = ||f-g||_p$$ とすると $(L^p , d_p)$ は距離空間となります。

距離空間 $(X,d)$ において，$a$ の $\varepsilon$ 近傍 を $$U(a , \varepsilon)=\{ x \mid d(x,a)< \varepsilon \}$$ と定めます。ただし，$a\in X$ で，$\varepsilon$ は正の実数とします。

$X = \mathbb{R}$，$d(x,y)=|x-y|$ の場合は， $$\begin{aligned} x \in U (a,\varepsilon) &\Longleftrightarrow d(x,a) < \varepsilon\\ &\Longleftrightarrow |x-a| < \varepsilon \end{aligned}$$

となります。

この表記を用いて，イプシロンエヌ論法・イプシロンデルタ論法 を，距離空間の視点で見てみます。

ここから少しむずかしいです。「開集合・閉集合・関数の連続性」について一般化を考えます。

1. ユークリッド空間における開集合・閉集合・関数の連続性
2. 距離空間における開集合・閉集合・関数の連続性
3. 一般の位相空間における開集合・閉集合・関数の連続性

と3段階あります。1は開区間，閉区間の意味と関連する話題で触れています。

以下では，3を意識しつつ2について解説します。今後の抽象論を意識した内容なので，難しく感じた人は読み飛ばしても構いません。

内点・触点

開集合・閉集合を具体的に定義するために，いくつか事前に定義をします。

若干抽象的ですので，難しいと思った方は先に後述する具体例から読んでみてください。

具体例

実数上の区間

$A=\{ x \in \mathbb{R} \mid -2 < x \leqq 4\}$ としましょう。

• 内点全体の集合は $\{ x \mid -2 < x < 4 \}$ である。
• 外点全体の集合は $\{ x \mid x < -2,4 < x \}$ である。
• 境界点は $x=-2,4$ である。
• 触点全体の集合は $\{ x \mid -2 \leqq x \leqq 4 \}$ である。
• 集積点全体の集合は $\{ x \mid -2 \leqq x \leqq 4 \}$ である。
• 孤立点は存在しない。

内点全体の集合は元の区間の不等号から $=$ を抜いたもの，触点全体の集合は元の区間の不等号に $=$ を追加したものになっていますね。

内点は開集合，触点は閉集合に対応する点だと思えそうです。

触点全体と集積点全体は一致し，孤立点はそもそも存在しません。これらの点を定義する意味は何でしょうか。次の例を見てみましょう。

離散的な集合

$B=\{ x \mid x= \frac{1}{n} , n \in \mathbb{Z}\}$ としましょう。

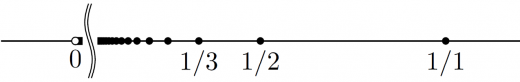
• 内点は存在しない。
• 外点全体の集合は $\{ x \mid x \neq \frac{1}{n} , n \in \mathbb{Z}\}$ である。
• 境界点全体の集合は $\{ x \mid x= \frac{1}{n} , n \in \mathbb{Z}\}$ である。
• 触点全体の集合は $\{ x \mid x= \frac{1}{n} , n \in \mathbb{Z}\} \cup \{0\}$ である。
• 集積点は $x=0$ である。
• 孤立点はある整数 $n$ を用いて $x=\frac{1}{n}$ となる点である。

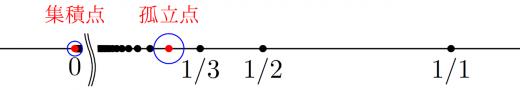
区間のときの例とは大きく異なりますね。

これら例から，触点の集合は集積点の集合＋孤立点の集合であることがわかるでしょう。（実際に証明してみましょう。）

近傍とイプシロンエヌ論法の関係を思い出すと，集積点とは(非自明な)数列の極限となる点を意味していることがわかります。

開集合と閉集合の定義

これまでの議論を通して開集合と閉集合を定義しましょう。

これまでの一連の流れを踏まえると，開集合と閉集合には次のような特徴付けができることがわかります。

1と2は，単純に各点が内点/触点であるかどうかを確かめる特徴付けになっています。

3は特殊です。4はかなり直観的でしょう。

この定義から非常に重要な連続関数の特徴付けが得られます。

開集合であることの証明が求められますが，これは距離空間・位相空間論においてベーシックかつ重要な手法となります。抽象的で難しいかもしれませんが，丁寧に読み進めてみてください。

上で示した定理と開集合と閉集合の特徴付け 4から次が従います。

これらの特徴付けは今後関数の連続性の証明で頻繁に用いられるので是非覚えてください。

今後は距離空間とは限らない一般の集合に対しても，開集合・閉集合を定めていきます。その後，連続関数の特徴付けを元に一般の集合に連続関数を定義します。

こうした一般化をすることで，素数全体の集合に開集合・閉集合を定めることができるようになります。おたのしみに。