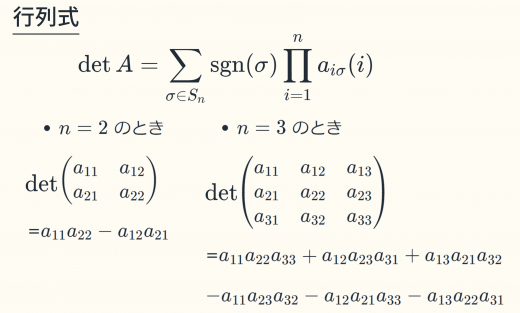線形代数 に関する79記事をまとめました。くわしくは各リンク先を見てください。
一次独立の定義
以下の条件を満たすとき,ベクトル
v1,…,vk
は一次独立であるという。
条件:i=1∑kcivi=0 を満たす実数 c1,…,ck の組は c1=⋯=ck=0 のみ。

→ベクトルの一次独立,一次従属の定義と意味
関数などの演算
f
が,任意の
a,b,x,y
に対して
f(ax+by)=af(x)+bf(y)
を満たすとき,f
のそのような性質を線形性と呼ぶ。
→高校数学における線形性の8つの例
O(0,0,0),A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3) を頂点とする四面体の体積は 61∣detM∣ となる。
→四面体の体積を求める2つの公式with行列式
n 本の線形独立なベクトル a1,a2,⋯,an を「用いて」正規直交基底を作る方法として,グラムシュミット(Gram–Schmidt)の正規直交化法がある。
→グラムシュミットの直交化法の意味と具体例
ロドリゲスの回転公式(ベクトル)
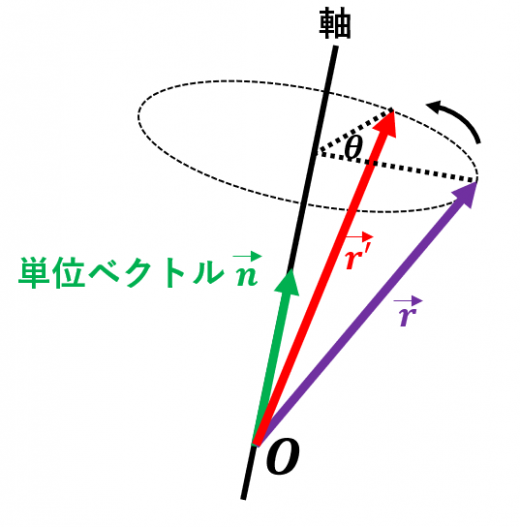 三次元空間において,n を軸として,r を θ 回転させた点 r′ は,
三次元空間において,n を軸として,r を θ 回転させた点 r′ は,
r′=(cosθ)r+(1−cosθ)(r⋅n)n+(sinθ)(n×r)
→ロドリゲスの回転公式(3次元の回転行列)
ヴァンデルモンド行列の定義
i=1,…,n について,i 列目が 1,xi,xi2,…,xin−1 である n×n 行列:
Vn=⎝⎛1x1x12⋮x1n−11x2x22⋮x2n−11x3x32⋮x3n−1⋯⋯⋯⋱⋯1xnxn2⋮xnn−1⎠⎞
をヴァンデルモンド行列と呼ぶ。
→ヴァンデルモンド行列式の証明と応用例
行列式とは,正方行列に対して決まる重要な量(スカラー)である。行列
A
の行列式を
detA
や
∣A∣
と表す。例えば
A=(a11a21a12a22)
の行列式は,
a11a22−a12a21
となる。
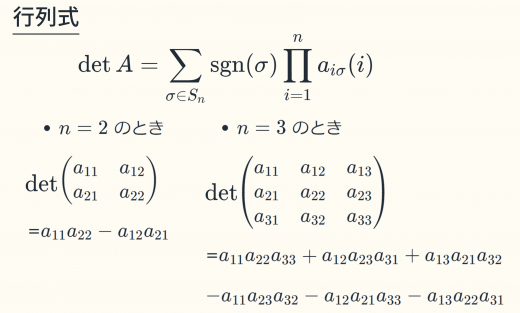
→行列式の基本的な定義・性質・意味
→バーコフ–フォン・ノイマンの定理
クラメル(Cramer)の公式
連立方程式
Ax=b
の解は,detA=0
のもとで,
xi=detAdetAi
である。ただし,xi
は
x
の第
i
成分であり,Ai は A の第 i 列の部分を b にしたもの。
→クラメルの公式の具体例と証明
固有値・固有ベクトルの定義
Ax=λx
が成立するとき
x
を
A
の固有ベクトル(英:eigenvector),λ
を
A
の固有値(英:eigenvalue)と言う。ただし,A は正方行列,x は 0
でないベクトル,λ は
スカラー。
→行列の固有値・固有ベクトルの定義と具体的な計算方法
行列積の定義(2×2の場合)
A=(a11a21a12a22),B=(b11b21b12b22)
のとき,
AB=(a11b11+a12b21a21b11+a22b21a11b12+a12b22a21b12+a22b22)
→行列の積の定義とその理由
行列
A,B,C,D
に対して
(A+BDC)−1=A−1−A−1B(D−1+CA−1B)−1CA−1
(ただし,行列の積が定義できるような適切なサイズ,および
A
などの逆行列の存在を仮定する)
特に
D=I
のとき,
(A+BC)−1=A−1−A−1B(I+CA−1B)−1CA−1
→逆行列の補助定理(Woodburyの恒等式)
転置行列の定義
行列に対して「行」と「列」を入れ替えた行列を転置行列と言う。
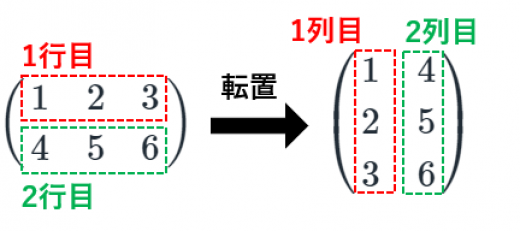
→転置行列の意味・重要な7つの性質と証明
行列における次元定理
A
を
m×n
実行列とするとき,
rankA+dim(KerA)=n
→次元定理の意味,具体例,証明
マトロイドの定義
有限集合
E
とその部分集合族
F
について,以下の3つの条件が成立するとき
(E,F) のペアをマトロイドと言う。
-
∅∈F
-
X⊆Y
かつ
Y∈F
なら
X∈F
-
X,Y∈F
かつ
∣X∣<∣Y∣
ならある
e∈Y∖X
が存在して
X+e∈F
→マトロイドの定義と具体例
半正定値行列の定義
実対称行列について,
- 固有値がすべて 0 以上であるとき,半正定値行列という。
- 固有値がすべて正であるとき,正定値行列という。
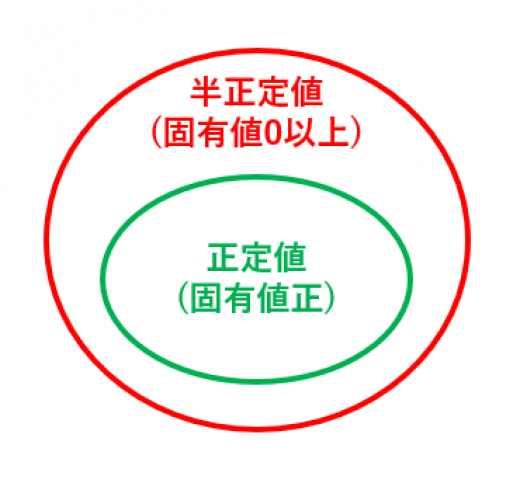
→半正定値対称行列の意味と性質【固有値・二次形式・分解・小行列式】
対称行列
行列 A が対称行列であるとは,転置しても変わらないことをいう。
つまり,A の i 行 j 列の成分を aij としたとき,aij=aji が成立する行列のことをいう。
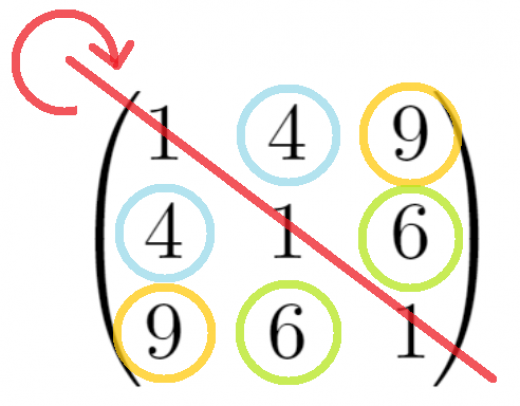
→対称行列の定義と性質~固有値と固有ベクトルの性質
ケーリー・ハミルトンの定理
正方行列 A に対して,det(A−λI) という λ の多項式の λ の部分を A に変えたものはゼロ行列になる。
→固有多項式とケーリー・ハミルトンの定理
A⊤A
が正則なとき,∥Ax−b∥
を最小にする
x
はただ一つであり,それは
正規方程式:A⊤Ax=A⊤b を解くことで得られる。
→正規方程式の導出と計算例
行列の対角化
与えられた正方行列
A
に対して,正則行列
P
をうまく取ってきて
P−1AP
を対角行列にする操作を対角化と言う。

→行列の対角化の意味と具体的な計算方法
トレースの定義
n×n
正方行列
A
に対して,対角成分の和
k=1∑nakk
を
A
のトレース(跡)と言い,trA
と書く。

→行列のトレースのいろいろな性質とその証明
2×2行列の逆行列
A=(acbd) の逆行列は,A−1=ad−bc1(d−c−ba)

→逆行列の定義・逆行列を求める2通りの方法と例題
連立一次方程式の解法であるガウスの消去法(掃き出し法)を解説します。ガウスの消去法は,アイデアが簡単かつ計算時間が短いので広く利用されています。
→ガウスの消去法(掃き出し法)による連立一次方程式の解き方
任意の行列に対してランク(rank)と呼ばれる重要な量が定まる。ランクにはいろいろな意味(性質)がある。
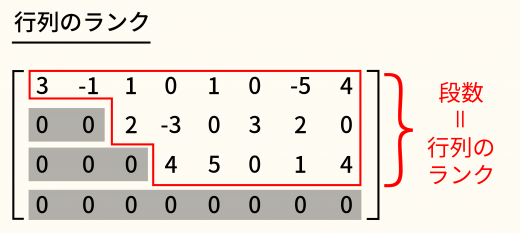
→行列のランク(rank)の8通りの同値な定義・性質
2つの対角化可能な行列 A,B について,
AB=BA⟺A と B は同時対角化可能
→同時対角化可能⇔交換可能の意味と証明
A
が正則なとき,
detT=detAdet(D−CA−1B)
D
が正則なとき,
detT=detDdet(A−BD−1C)
→ブロック行列の行列式,逆行列の公式と証明
直交行列の同値な5つの定義
-
U⊤=U−1
-
U の n 本の行ベクトルが正規直交基底をなす
-
U の n 本の列ベクトルが正規直交基底をなす
-
任意の x∈Rn に対して ∥Ux∥=∥x∥
-
任意の x,y∈Rn に対して Ux⋅Uy=x⋅y
→直交行列の5つの定義と性質の証明
二次形式とは,二次の項のみからなる多項式のこと。例えば,3x12−2x1x2+4x22
は二次形式。
→二次形式の意味,微分,標準形など
操作1. 交換
ある行と別の行を交換する。
例. 1行目と3行目を交換する
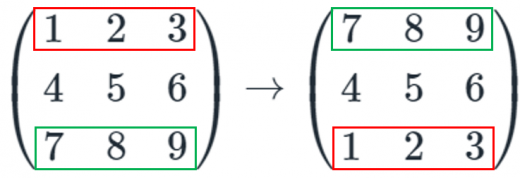
→行列の基本変形の意味と応用(rank・行列式の計算)
カーネル(核)の定義
行列
A
に対して,Ax=0
を満たすベクトル
x
の集合を
A
のカーネル(または核)と言い,KerA
と書くことが多い。
→行列のカーネル(核)の性質と求め方
A⊤A の固有値分解と AA⊤ の固有値分解ができれば,A の特異値分解 A=UΣV が計算できる。
→特異値分解の定義,性質,具体例
性質1
∥A∥F2=tr(AA⊤)=tr(A⊤A)
→行列のフロベニウスノルムとその性質
- pfA=M∑sgn(M)(i,j)∈M∏aij
- permA=σ∑i=1∏naiσ(i)
- hafA=M∑(i,j)∈M∏aij
→行列のパフィアン,パーマネント,ハフニアン
定理
an+k=pk−1an+k−1+pk−2an+k−2+⋯+p1an+1+p0an
という漸化式について,k
次方程式
ϕ(λ)=λk−pk−1λk−1−pk−2λk−2−⋯−p1λ−p0=0
を特性方程式と言う。特性方程式の解
λ1,⋯,λk
が全て異なるとき,数列
an
の一般項は
an=C1λ1n+C2λ2n+⋯+Ckλkn
と表せる(C1,⋯,Ck
は初期条件によって決まる定数)。
→漸化式の特性方程式の意味とうまくいく理由
ビネ・コーシーの定理
A
を
m×n
行列,B
を
n×m
行列とする。
m≤n
なら,
detAB=S∑detA[S]detB[S]
→ビネ・コーシーの定理とその証明
任意の正方行列
A
に対して,ある正則行列
P
が存在して,P−1AP=J
(J
はジョルダンブロックを対角に並べた行列)になるようにできる。
→ジョルダン標準形の意味と求め方
行列の指数関数(eの行列乗)の定義
正方行列
A
に対して,eA を以下の式で定義する。
eA=I+A+2!A2+3!A3+⋯
→行列の指数関数とその性質
対角化(またはジョルダン標準形)を用いて正方行列の
n
乗を計算できる。
→行列のn乗の求め方と例題
正則行列とは
正方行列 A について,AB=BA=I(単位行列)となる行列 B が存在するとき,A を正則行列と言う。
→行列が正則であることの意味と5つの条件
→上三角行列と下三角行列の意味と6つの定理
各要素が
1
または
−1
で,各行が互いに直交するような正方行列をアダマール行列 (Hadamard matrix) と言う。
→アダマール行列の定義と性質
⎝⎛13000246000579000810120001113⎠⎞
のように,
対角成分とそれに隣接する成分(副対角成分)以外が
0
であるような正方行列を三重対角行列と言う。
→三重対角行列の特殊形の固有値は綺麗
対角化可能な正方行列
A について,全ての固有値が
−1 より大きく
1 より小さいとき,
k=0∑∞Ak=I+A+A2+⋯
は (I−A)−1 に収束する。
→行列の無限等比級数
「テンソル」という言葉には,
- 代数学における「ベクトル空間のテンソル積」
- 物理や微分幾何における「テンソル場」
- その他,数の高次元配列としてのテンソルなど
といった,さまざまな意味がある。
→テンソルとは何か Part.1
交代行列の定義
交代行列とは,⎝⎛0−1−210−3230⎠⎞ のように,A⊤=−A を満たす正方行列,つまり転置するとマイナス1倍になる行列のこと。

→交代行列の定義と性質
「テンソル」という言葉には,
- 代数学における「ベクトル空間のテンソル積」
- 物理や微分幾何における「テンソル場」
- その他,数の高次元配列としてのテンソルなど
といった,さまざまな意味がある。
→テンソルとは何か Part.2
例題
次の連立微分方程式を解け。
⎩⎨⎧dtdx1(t)=x1(t)−2x2(t)dtdx2(t)=x1(t)+4x2(t)
ただし x1(0)=1,x2(0)=−2 とする。
→連立微分方程式の3通りの解き方
行列の指数関数の定義
正方行列 A に対して,eA は
eA=I+A+2!A2+3!A3+⋯
と定義される。
→行列の指数関数の計算方法
巡回行列
⎝⎛xzyyxzzyx⎠⎞ のように,「左上~右下方向」に同じ値が並んだ行列を巡回行列(循環行列,Circulant matrix)という。
→巡回行列の固有値・固有ベクトルと行列式
射影行列の定義
P2=P を満たす正方行列 P を射影行列という。
→射影行列のイメージと楽しい公式
エルミート行列
(12−i2+i1) のように「転置して複素共役をとっても変わらない行列」を エルミート行列(Hermitian matrix)という。以下の性質がある:
- 固有値は実数
- 固有ベクトルたちは直交
- ユニタリ行列で対角化可能
→エルミート行列とその性質,ユニタリ対角化の証明
ユニタリ行列の定義
-
U∗=U−1
-
U の n 本の行ベクトルが正規直交基底をなす
-
U の n 本の列ベクトルが正規直交基底をなす
-
任意の x∈Cn に対して ∥Ux∥=∥x∥
-
任意の x,y∈Cn に対して Ux⋅Uy=x⋅y
→ユニタリ行列の定義と性質の証明
シルベスターの慣性法則
1(大雑把な言い方):
多変数の二次関数を平方完成したとき,二乗の係数のプラス・0・マイナスの数は平方完成のやり方によらない。
2(数式で正確に):
対称行列 A に対して,正の固有値の数,0 の固有値の数,負の固有値の数を p(A),z(A),n(A) とおく。正則行列 S を用いて B=S⊤AS という関係が成立するなら,p(A)=p(B),z(A)=z(B),n(A)=n(B)
3(簡潔な言い方):
互いに合同な行列の固有値の各符号の数は同じ。
→シルベスターの慣性法則の意味と証明
単位行列の定義
対角成分が 1 で,それ以外の成分が 0 である正方行列を単位行列と言う。
- サイズ2の単位行列:(1001)
- サイズ3の単位行列:⎝⎛100010001⎠⎞
→単位行列の意味と性質,1との比較
定理1
任意の m×n 複素行列 A に対して,以下の4つの条件を満たす n×m 複素行列 B がただ1つ存在する。
- ABA=A
- BAB=B
- (AB)∗=AB
- (BA)∗=BA
→一般化逆行列(ムーア・ペンローズの疑似逆行列)
定理1(最小ノルム解)
Ax=b を満たす x の中で ∥x∥2 を最小にする解 x∗ がただ1つ存在し,
x∗=A⊤(AA⊤)−1b
ただし,A は行ベクトルが線形独立な m×n 行列,x は n 次元ベクトル,b は m 次元ベクトルとする。
→最小ノルム解の導出と図による理解
QR分解
任意の正方行列 A に対して,あるユニタリ行列 Q と上三角行列 R が存在して A=QR
と分解できる。
→行列のQR分解と応用(固有値・最小二乗法)
正規行列の定義
正方行列 A が AA∗=A∗A を満たすとき,A を正規行列(normal matrix)と言う。
→正規行列の意味と3つの代表例
余因子とは
正方行列に対して
「i 行目と j 列目を除いた行列」の行列式に (−1)i+j をかけたもの
を(i,j) 余因子と言う。
→余因子と余因子行列
スペクトル分解(射影行列による表現)
任意の正規行列 A は以下のように分解できる。
A=i=1∑NλiPλi
ただし,λ1,...,λN は A の相異なる固有値すべてで,Pλi は固有値 λi の固有空間への射影行列。
→行列のスペクトル分解
内積空間(計量ベクトル空間)
V を実ベクトル空間とする。x,y∈V に対して実数を定める関数
⟨x,y⟩:V×V→R が以下の1~4を満たすとき,⟨ , ⟩ を内積といい,V を内積空間(計量ベクトル空間)という。
- ⟨x,y⟩=⟨y,x⟩(エルミート性)
- ⟨x+ay,z⟩=⟨x,z⟩+a⟨y,z⟩(x,y,z∈V,a∈R)(線型性)
- ⟨x,x⟩≧0(正定値性)
- ⟨x,x⟩=0⇒x=0(非退化性)
→内積の入ったベクトル空間~内積空間(計量ベクトル空間)
定理
V を内積空間とする。ここで内積を ⟨,⟩ で表す。
V の部分空間 W の直交補空間 W⊥ を
W⊥={v∈V∣∀w∈W,⟨v,w⟩=0}
と定める。
※ 内積空間よりも広く,双線型形式というものが定義されたベクトル空間であれば,直交補空間を定義することができます。
→直交補空間の性質
定理
実ノルム空間 V について,中線定理
∥x+y∥2+∥x−y∥2=2(∥x∥2+∥y∥2)
が成立するとき,
⟨x,y⟩=41(∥x+y∥2−∥x−y∥2)
により内積が定まる。
またこうして得られた内積において
⟨x,x⟩=∥x∥
となる。
→ノルム空間はいつ内積空間になるのか?~証明
定義
detA=σ∈Sn∑sgn(σ)i=1∏naiσ(i)=σ∈Sn∑sgn(σ) a1σ(1)a2σ(2)⋯anσ(n)
→攻略! 行列式計算~その2~
定義
detA=σ∈Sn∑sgn(σ)i=1∏naiσ(i)=σ∈Sn∑sgn(σ) a1σ(1)a2σ(2)⋯anσ(n)
→攻略! 行列式計算~その1:基本練習問題8パターン
定義
detA=σ∈Sn∑sgn(σ)i=1∏naiσ(i)=σ∈Sn∑sgn(σ) a1σ(1)a2σ(2)⋯anσ(n)
→攻略! 行列式計算~その3:固有値を活用した計算
岩澤分解
正則な 2×2 行列は,回転行列・対角行列・(対角成分が 1 である)上三角行列の積,つまり
(cosθ−sinθsinθcosθ)(x00y)(10t1)
という形に分解できる。
→岩澤分解
定義
行列 A の最小多項式とは,最高次数の係数が 1 の多項式 f であって f(A)=O となるもののうち次数が一番小さいものである。
→行列の最小多項式
行列の上三角化
与えられた正方行列
A
に対して,ユニタリ行列(直交行列)
P
をうまく取ってきて
P−1AP
を上三角行列にできる。
※ A の固有値が全て実数の場合,直交行列で三角化できる。
→行列の上三角化~グラム・シュミットの直交化法を用いて
定義
ベクトル空間 V の2つの基底 {v1,…,vn},{v1′,…,vn′} について
(v1′⋯vn′)=(v1⋯vn)P
を満たす n×n 正方行列 P を基底の変換行列という。ただし,
- (v1′⋯vn′) とは,n 本の縦ベクトル v1′,...,vn′ を横に並べた n×n 行列
- (v1⋯vn) とは,n 本の縦ベクトル v1,...,vn を横に並べた n×n 行列
→基底の変換行列~定義と具体例
定義
ベクトル空間 V と W の基底をそれぞれ {v1,⋯,vn} と {w1,⋯,wm} とする。
ベクトル空間の線型写像 f:V→W について
⎩⎨⎧f(v1)=a11w1+a21w2+⋯+am1wmf(v2)=a12w1+a22w2+⋯+am2wm⋮f(vm)=a1nw1+a2nw2+⋯+amnwm
と表されたとする。この係数を並べた行列
⎝⎛a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎠⎞
を{v1,⋯,vn} と {w1,⋯,wm} による線型写像の表現行列という。
つまり表現行列とは,
(f(v1)⋯f(vn))=(w1⋯wm)A
と表すことができる行列 A のことである。
→線型写像の表現行列とその例
随伴行列の定義
行列
A
に対して,転置して複素共役を取った行列 A∗=A⊤ を,随伴行列(共役転置行列・エルミート転置行列)という。
→随伴行列の定義・重要な性質
線型写像
V,W を K 上のベクトル空間とする。(K は体,例えば R や C など)
写像 p:V→W が
- ϕ(v1+v2)=ϕ(v1)+ϕ(v2)(v1,v2∈V)
- ϕ(cv)=cϕ(v)(a∈K,v∈V)
を満たすとき ϕ を線型写像(線型変換)という。
→線型写像とその例~行列・一次変換など
定義
V をベクトル空間,W を V の部分ベクトル空間とする。
V 上の二項関係 ∼ を v∼v′⟺v−v′∈W で定義すると,∼ は同値関係を成す。V をこの同値関係で割った商集合はベクトル空間の構造を持つ。
これを商ベクトル空間といい,V/W と書く。
→商ベクトル空間
対角化(ジョルダン標準形)は表現行列により説明ができる。
→表現行列の観点から見た対角化
定理
対角化可能な行列 A,B について次の2つは同値である。
- AB=BA を満たす。
- A,B は同時対角化である。つまり,ある正則行列 P があって PAP−1 と PBP−1 は対角行列にできる。
→同時対角化の練習問題~院試の問題を通して
定理
n×n 行列 A に対して,固有値 λ の固有ベクトル全体(に 0 ベクトルを加えたもの)の集合はベクトル空間になる。これを λ に対する固有空間 という。
→行列の固有空間とその性質
群構造を成す行列の集合を行列群という。代表的なものに GLn(C),SLn(C),O(n),U(n) がある。
→一般線型群・ユニタリ群・直交群
定理
有限次元ベクトル空間 V の部分空間 W について,次が成り立つ。
- dimV≥dimW
- dimV=dimW であれば V=W になる。
→線型代数の有名事実~部分空間と次元の関係について

 三次元空間において, を軸として, を 回転させた点 は,
三次元空間において, を軸として, を 回転させた点 は,