グラフ理論
更新
グラフ理論 に関する22記事をまとめました。くわしくは各リンク先を見てください。
任意の(穴のない)多面体について,
が成立する。ただし,頂点の数を , 辺の数を , 面の数を とした。

連結なグラフにおいて,
- 一筆書きして戻ってこれる 全ての頂点の次数が偶数
- (スタートとゴールが異なるような)一筆書きができる 次数が奇数であるものがちょうど2つ
組合せの良問を紹介します。証明だけでなく,考え方や重要なテクニックも紹介します。
言葉で表現すると大変なのでグラフを用います。つまり,6人をそれぞれ点で表し,知り合いを赤い線で結び,知らない人を青い線で結びます。このグラフにおいて赤い三角形か青い三角形が存在することを示せばよいです。
グラフ の頂点 の次数を とおくとき,
主張1:
- グラフとは,頂点の集合 と二点間を結ぶ辺の集合 のペアです。
- などと表します。
- グラフはつながりの構造を表すモデルです。図における二つのグラフは同じとみなします。
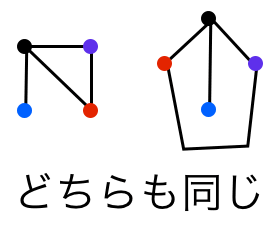 頂点の置き方やどのような曲線で結ばれているかは考えません(図では分かりやすくするために頂点に色をつけています)。
頂点の置き方やどのような曲線で結ばれているかは考えません(図では分かりやすくするために頂点に色をつけています)。

人の男性と 人の女性がいて,各人の異性に対する希望順位が与えられた状況を考えます。全員が「それなりに幸せになれる」ような結婚のペアの決め方(完全マッチング)を求めるのが目標です。
マッチング について以下を満たすとき 道 は増加道であるという。
- の出発点と到着点がマッチングの端点でない
- 交互路である( に含まれていない枝と含まれている枝を交互に使う)
任意の地図は四色で塗り分けることができる。
頂点数 のグラフが三角形を含まないとき,その辺数は 以下である。また,任意の に対して,辺数が であるような三角形を含まないグラフが存在する。
Hall(ホール)の結婚定理:頂点集合が と分割された二部グラフ に対して,以下は同値。
条件1: の頂点を全てカバーするマッチングが存在する
条件2(Hallの条件):任意の の部分集合 に対して,
ただし, は と辺でつながっている頂点の集合。
完全グラフ および完全二部グラフ は平面的グラフでない。
-
最小全域木 を求める。
-
の枝をコピーしたグラフを一筆書きで一周する。
-
一回通ったとこはショートカットすることで,全都市をちょうど一回巡る閉路にする。
点(母点)がいくつか与えられたとき,どの点に一番近いかによって平面を分割したものをボロノイ図(Voronoi diagram)と言う。
穴のない 角形の全領域を監視するために必要な監視カメラの台数は高々 台
-
,
-
以外の各頂点 について,
- 隣接行列
- 点枝接続行列
- ラプラシアン行列
- Tutte行列
深さ優先探索とは「とにかく行けるとこまで行ってそれ以上進めなくなったら一歩戻ってそこから探索する」という探索方法。
幅優先探索とは「出発点に近い点から順に探索する」という探索方法。
深さ優先探索を2回すれば強連結成分分解できる。
有限集合 とその部分集合族 について,以下の2つの条件が成立するとき のペアをデルタマトロイドと言う。
-
は空でない。
-
任意の と任意の に対して,ある が存在して,
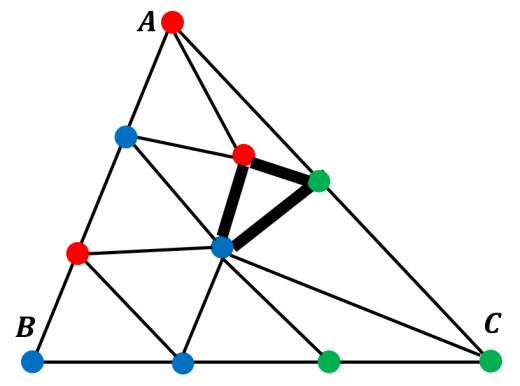
- 大きい三角形 がある。
- この三角形の周または内部にいくつかの点があり,小さい三角形たちに分割されている。
- 頂点 および各点は赤・青・緑のいずれかで塗られている。ただし以下を満たす:
- は異なる色
- 辺 上の点は または と同じ色
- 辺 上の点は または と同じ色
- 辺 上の点は または と同じ色
このとき, つの頂点の色が相異なるような小さい三角形が存在する。
無向グラフ に対して, の全域木の個数は, のラプラシアン行列の任意の余因子と等しい。





