式の計算 に関する43記事をまとめました。くわしくは各リンク先を見てください。
1. (x+a)(x+b)=x2+(a+b)x+ab
→乗法公式(式の展開公式)19個まとめ
分母の有理化はした方がきれいになる場合もあるが,必ずしないといけないものではない。
→分母の有理化や実数化について
→二重根号の外し方・外せないものの判定
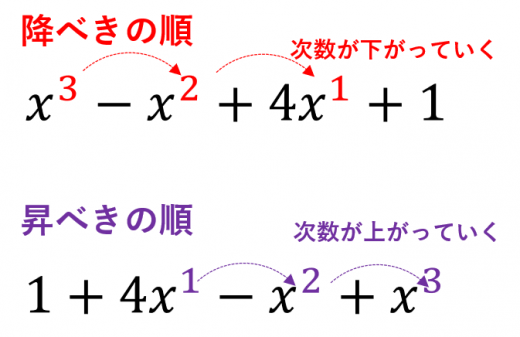
降べきの順とは,次数が下がって行くような式の表し方。
降べきの順で表した例:
x3−x2+4x+1
昇べきの順とは,次数が上がって行くような式の表し方。
昇べきの順で表した例:
1+4x−x2+x3
→降べきの順と昇べきの順について
組立除法とは,多項式の割り算において商と余りをすばやく求める手法です。

→組立除法のやり方と例題3問
平方完成とは
x2+2x+3=(x+1)2+2
のように,二次式を a(x−p)2+q の形に変形することを平方完成と言う。

→平方完成のやり方といくつかの発展形
多項式の割り算
与えられた多項式 A(x),B(x) に対して,
- A(x)=B(x)Q(x)+R(x)
- Rの次数<Bの次数
を満たす多項式 Q(x),R(x) が1つに決まる。Q(x) を商,R(x) を余りと言う。
→多項式の割り算の二通りの計算方法と例題
循環小数とは,0.22222… のように「途中からひたすら同じ列を繰り返す」ような小数のことです。
→循環小数の意味と分数で表す方法など
整数部分と小数部分
- 小数点以下を切り捨てたものを整数部分と言います。
- 残った部分を小数部分と言います。
 例えば 3.14 の整数部分は 3 で,小数部分は 0.14 です。
例えば 3.14 の整数部分は 3 で,小数部分は 0.14 です。
→整数部分と小数部分の意味と例題
ルートの近似値
- 2≒1.41421356(一夜一夜に人見頃)
- 3≒1.7320508(人並みにおごれや)
- 5≒2.2360679(富士山麓オウム鳴く)
- 6≒2.44949(によよくよく)
- 7≒2.64575(菜に虫いない)
→ルート2,ルート3,ルート5の覚え方など
単項式の定義
単項式とは,数,文字,およびそれらの積として表される式のこと。
→単項式,多項式,整式
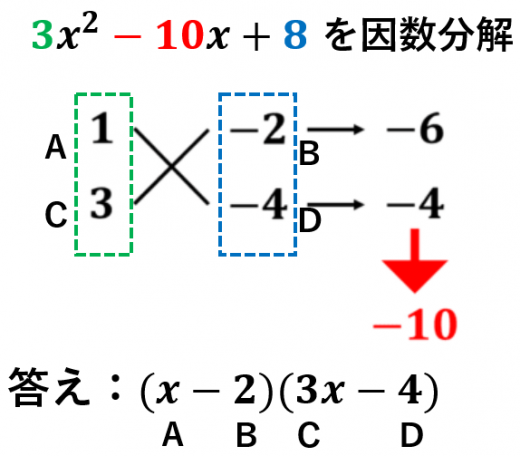
たすきがけ
たすきがけとは,3x2−10x+8 のような二次式を因数分解するための方法です。
→たすきがけによる因数分解のやり方・例題・他の方法
定義1
単項式や多項式のことを総称して整式と呼びます。
→単項式・多項式や次数・係数などの定義と問題例
- 非負性 : 必ず 0 以上である。 ∣a∣≧0
- 非退化性 : a=0 のときに,またそのときのみ ∣a∣=0 になる。
- 偶性 : 原点に関して対称である。 ∣−a∣=∣a∣
- 劣加法性(三角不等式) : ∣a+b∣≦∣a∣+∣b∣
- 冪等性(べきとうせい) : 操作を複数回繰り返しても結果が変わらない。 ∣∣a∣∣=∣a∣
- 乗法性 : ある2数の積の絶対値と,その2数の絶対値の積は同じ値になる。 ∣ab∣=∣a∣・∣b∣
→絶対値の意味と性質・記号の外し方・絶対値を含む式の計算方法
分数式の計算方法をわかりやすく解説します。分数式の計算に迷ったら「普通の分数」の計算方法を思い出すとよいです。
→分数式の基本的な計算と例
2乗の因数分解公式
x2+(a+b)x+ab=(x+a)(x+b)x2+2xy+y2=(x+y)2x2−2xy+y2=(x−y)2x2−y2=(x−y)(x+y)
→因数分解の公式とテクニック一覧
交代式とは,どの2つの変数を入れ替えても
−1
倍になるような式のことです。例えば
a2−b2
という式は,a
と
b
を入れ替えると
b2−a2
となり,元の式の
−1
倍になるので交代式です。
→交代式の因数分解と実践的な例題
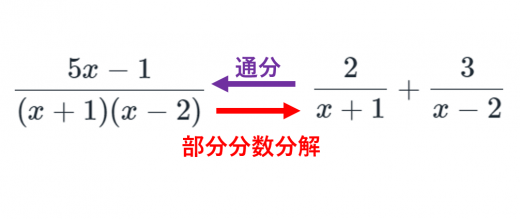
部分分数分解とは,
(x+1)(x−2)5x−1=x+12+x−23
のように「いくつかの分数のたし算(または引き算)に分解する」こと。つまり,通分の逆。
→部分分数分解の3通りの方法
a+b±c1 の分母を有理化したいときは,分母分子に a+b∓c をかけていつもの分母の有理化に帰着させる
→分母に項が3つある場合の有理化
調和平均とは
2÷(a1+b1)
を
a
と
b
の調和平均と呼ぶ。
→調和平均の意味と性質まとめ
1:全ての対称式は基本対称式の多項式で表せる。
2:特に,xn+yn
の値は
x+y
と
xy
の値が分かれば機械的に計算できる。
3:さらに,xn+xn1
の値は
x+x1
の値が分かれば機械的に計算できる。
4:基本対称式は解と係数の関係と相性がよい。
→2変数の対称式と基本対称式の4つの性質
対称式とは,どの2つの変数を交換しても変わらない多項式のことです。
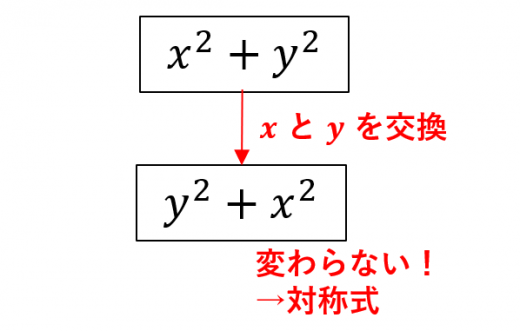 例えば,x2+y2 という式で x と y を交換すると y2+x2 になります。x2+y2=y2+x2 なので多項式として変わっていません。よって x2+y2 は対称式です。
例えば,x2+y2 という式で x と y を交換すると y2+x2 になります。x2+y2=y2+x2 なので多項式として変わっていません。よって x2+y2 は対称式です。
→対称式について覚えておくべき7つの公式
加比の理(等式バージョン)
値が等しい分数は,分母同士・分子同士を足しても等しい。つまり,
ab=cd のとき
ab=cd=a+cb+d
→加比の理と傾きによる証明
2 は無理数である。
より一般に,平方数でない正の整数 n に対して n は無理数である。
→ルート2が無理数であることの4通りの証明
a
の近似値の求め方の概要:
- x2≒a となりそうな簡単な x を探す。
- x2>a ならもう少し小さい x で再挑戦。
x2<a ならもう少し大きい x で再挑戦。
→ルートの近似値を計算する素朴な方法とコツ
54321のルートを筆算する方法
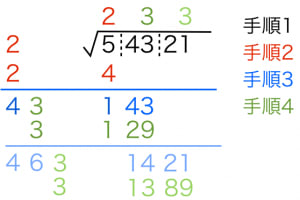
-
まず 54321 と右側に書く。小数点を基準に2桁ずつ区切っていく。
-
二乗して「右側の最も左のブロック(この例だと 5)」以下となるような最大の整数(この場合 2)を求める。その数を右側に1箇所,左側に2箇所書く。また,計算結果(この場合 22=4)を右側に書く。
-
左側は足し算,右側は引き算。
-
左側の数(この場合 4)の末尾に N をくっつけたもの ×N が右側の次のブロックまで取ったもの(この場合 143)以下となるような最大の整数を求める。その数を右側に1箇所,左側に2箇所書く。この場合,43×3=129 であり,3 が該当する。また,その計算結果(この場合 129)を右側に書く。
-
以下,3と4を必要なだけ繰り返す。
54321
の近似値が
233
と求まりました。実際,2332=54289
です。
→開平法のやり方と原理
「複素数の範囲での」因数分解の問題
- x2−2x+3
- x4−x2−2
- x2+y2+z2−xy−yz−zx
→複素数の範囲での因数分解の例題4問
分母の有理化
31→33 のように,分母を有理数にする変形を分母の有理化と言います。
→分母の有理化の方法と問題例6問(中学から高校まで)
分数の分母や分子に分数があるものを繁分数という。
また,以下のような形の数を連分数という。
a0+a1+a2+a3+⋯b3b2b1
→「分数の分数」の形をした繁分数・連分数
問題
二次方程式 x2−x−1=0 の異なる2つの実数解をそれぞれ α,β とする。
(1) α+β の値を求めよ。
(2) α10+β10 の値を求めよ。
(3) α+β,α2+β2,α3+β3,⋯,α2022+β2022 の2022個の実数のうち,整数であって3の倍数であるもの個数を求めよ。
→式の計算・二次関数分野:練習問題一覧|入試数学コンテスト過去問集
→黄金進法の意味とおもしろい定理
→行列・関数・多項式に共通する有名な性質
- パターン1-A:普通に因数定理が使える場合
- パターン1-B:二次式×二次式に分解できる場合
- パターン2:相反方程式
- パターン3:複二次式
- パターン4:方程式が解けない場合
→四次式の因数分解の5パターン
原始多項式の定義
a0,a1,⋯,an の最大公約数が 1 のとき,f(x) を原始多項式と呼ぶ。
→原始多項式とその積について
対称式の展開した式に,ka2 という項があれば kb2,kc2 という項もあります。 ka2b という項があれば kab2,kb2c,kbc2,kc2a,kca2 もあります。
→対称式を素早く正確に展開する3つのコツ
問題
p
と
q
を自然数として,
qp=1−21+31−41+⋯−13181+13191
が成立するとき
p
は
1979
の倍数となることを証明せよ
→交代和にまつわる数オリの問題
n
個の変数
x1,⋯,xn
について
i
次の基本対称式を
ei(x1,⋯,xn)
i
乗和を
pi(x1,⋯,xn)=x1i+⋯+xni
とする。このとき,
kek=i=1∑k(−1)i−1ek−ipi
→ニュートンの恒等式とその証明
対称式の基本定理
対称式は基本対称式の多項式として表せる。その表し方は一通りである。
→対称式の基本定理の証明
-
階乗:n! は 1 から n までの整数を全てかけあわせたもの
-
二重階乗:n!! は一つおきにかけあわせたもの
-
超階乗:n$ は n! の肩に n! を n!−1 個乗せたもの
→階乗,二重階乗,超階乗
足し算,かけ算,べき乗を一般化した
ハイパー演算というものがある。
→ハイパー演算子とクヌースの矢印
チューリングマシンとは
チューリングマシンとは,次の6つの要素の組として定義される,ある規則にしたがって自動で計算を進める数学的なモデルのこと:
(Q,Σ,δ,q0,qacc,qrej)
→チューリングマシンの定義とそれに関連する話
定理1
定数
aij(1≤i≤k,1≤j≤ni)
をうまく選べば
Q(x)P(x)=i=1∑kj=1∑ni(x−xi)jaij
→ヘビサイドの展開定理
n乗の差の因数分解公式
an−bn=(a−b)(an−1+an−2b+⋯+abn−2+bn−1)
→因数分解公式(n乗の差,和)




 例えば の整数部分は で,小数部分は です。
例えば の整数部分は で,小数部分は です。

 例えば, という式で と を交換すると になります。 なので多項式として変わっていません。よって は対称式です。
例えば, という式で と を交換すると になります。 なので多項式として変わっていません。よって は対称式です。





