データの分析，確率

以下の式で定義される $E[X]$ を期待値と言う：

$E[X]=\displaystyle\sum_{i=1}^np_ix_i$

• 平均値とは，「合計」÷「個数」
• 中央値とは，「大きさ順に並べた真ん中」
• 最頻値とは，「一番たくさんある数」

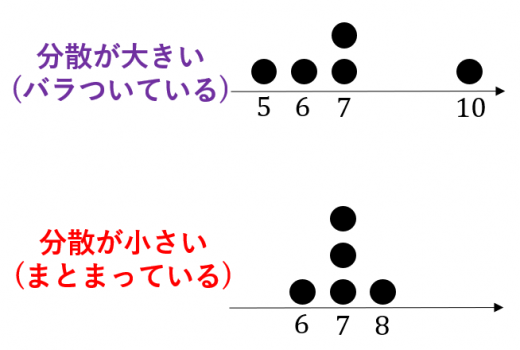
分散とは，データの「バラつきの大きさ」「散らばりの大きさ」を表す指標。

• 分散が大きい → バラつきが大きい，平均から遠いものが多い
• 分散が小さい → バラつきが小さい，全部が平均に近い，まとまっている

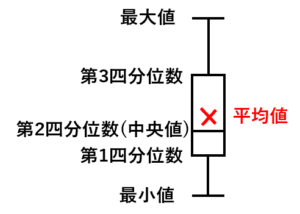
箱ひげ図とは，図のように「最大値・最小値・四分位数」の情報を表現したグラフです。箱ひげ図には平均値の情報が含まれることもあります。

箱ひげ図を見れば，データの分布をおおまかに把握できます。

「$A$ が起こる確率」＝ $1$－「$A$ が起こらない確率」

標準偏差とは，データの「バラつきの大きさ」「散らばりの大きさ」を表す指標。

• 標準偏差が大きい → バラつきが大きい，平均から遠いものが多い
• 標準偏差が小さい → バラつきが小さい，全部が平均に近い，まとまっている

相関係数 $\rho$ は， $$\rho=\dfrac{\dfrac{1}{n}\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\dfrac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2}{\sqrt{\dfrac{1}{n}\sum_{i=1}^n(y_i-\overline{y})^2}}}$$ で定義される。標準偏差 $\sigma_X,\sigma_Y$ と共分散 $\sigma_{XY}$ を使うと， $$\rho=\dfrac{\sigma_{XY}}{\sigma_X\sigma_Y}$$ とも書ける。

確率 $p$ で成功するような試行を独立に $n$ 回反復して行ったとき，$n$ 回のうち $k$ 回成功する確率は，

${}_n\mathrm{C}_kp^k(1-p)^{n-k}$

確率変数 $X,Y$ と期待値に関して以下が成立する： $$E[X+Y]=E[X]+E[Y]$$ より一般に，以下が成立する： $$\displaystyle E[\sum_{i=1}^nX_i]=\sum_{i=1}^nE[X_i]$$

$P(X)P(Y|X)=P(Y)P(X|Y)=P(X\cap Y)$

壺（つぼ）に赤玉が $a$ 個，白球が $b$ 個入っている。その中から玉を1つ無作為に取り出し，選んだ玉を壺に戻した上で選んだ玉と同じ色の玉を1つ壺に加える。

この試行を $n$ 回繰り返す。$n$ 回目に赤玉が選ばれる確率は $p_n=\dfrac{a}{a+b}$

$23$ 人いれば，その中に「同じ誕生日である二人組」が $50$ ％以上の確率で存在する。

$P(n)=(1-p)^{n-1}p$

で表される離散型確率分布を幾何分布と言う。

3人の巴戦では，最初に戦う2人が有利で，勝つ確率は $\dfrac{5}{14}\fallingdotseq 35.7$％ である。残った1人の勝つ確率は $\dfrac{4}{14}\fallingdotseq 28.6$％ である。

0. 三つの扉がある。一つは正解。二つは不正解。

1. 挑戦者は三つの中から一つ扉を選ぶ。

2. 司会者（モンティ）は答えを知っており，残り二つの扉の中で不正解の扉を一つ選んで開ける。

3. 挑戦者は残り二つの扉の中から好きな方を選べる。このとき扉を変えるべきか？変えないべきか？

$n$ 種類，等確率のコンプガチャで全ての景品を集めるのに必要な回数の期待値は $n\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots +\dfrac{1}{n}\right)$ である。

事象 $A_1,A_2,\cdots,A_n$ に対して

$P(A_1\cup A_2\cup\cdots\cup A_n)\leq \displaystyle\sum_{i=1}^nP(A_i)$

• 平均値は平均二乗誤差（MSE，Mean Squared Error）を最小にする。
• 中央値は平均絶対誤差（MAE，Mean Absolute Error）を最小にする。