複素数 に関する20記事をまとめました。くわしくは各リンク先を見てください。
共役複素数
複素数 a+bi に対して,a−bi のことを共役な複素数と言います(ただし a,b は実数)。
例えば,2+3i に対して共役な複素数は 2−3i です。
→共役複素数の覚えておくべき性質
複素数がなぜ必要なのか?
→複素数は,自然界の法則や数学の定理を記述するのに非常に便利だから。
→複素数の存在意義と様々な例
定理
複素数のルートは2つある。それらは複素数平面で原点対称な位置に存在する。
→複素数のルートを求める2通りの方法
複素数の絶対値
複素数 z=a+bi の絶対値 ∣z∣ を ∣z∣=a2+b2 で定める。
→複素数の絶対値の定義といろいろな性質
→複素数,虚数,純虚数,実数
ω
の多項式は必ず
Aω+B
という形まで計算できる。特に試験問題では
A=0
となる場合が圧倒的に多い。
→1の三乗根オメガを用いた計算と因数分解
複素数
α,β,γ
に対応する複素数平面上の3点
A(α),B(β),C(γ)
が正三角形となる必要十分条件は,
(α−β)2+(β−γ)2+(γ−α)2=0
→複素数平面において正三角形となる条件
複素数
α,β
に対応する二点
A(α),B(β)
と原点
O
でつくられる三角形
OAB
の面積は,
41∣αβ−αβ∣=21∣Im(αβ)∣
→複素数平面における三角形の面積
- z=z∣z∣2
特に,∣z∣=1 のとき,z=z1
→複素数平面の基本的な公式集
極形式
複素数を a+bi ではなく
r(cosθ+isinθ)
という形で表すことがあります。これを複素数の極形式と言います。
→複素数平面における極形式と回転
1のn乗根の性質
-
1の n 乗根は複素数平面の単位円周上に等間隔で並ぶ。
-
1の
n
乗根は全部で
n
個あるが,それらの和は0である。
-
1の n 乗根のうちどれでもよいので1つを ζ とおくと ζ=ζn−1=ζ1
→1のn乗根の性質と複素数平面
数 a に対して,n 乗して a になるような数を a の n 乗根という。
→累乗根の定義と具体例
問題
複素数平面において,
∣z−3∣+∣z+3∣=4
を満たす複素数 z 全体を C とする。
(1) α が C 上を動くとき,α の軌跡によって囲まれる部分の面積を求めよ。
(2) α が C 上を動くとき,α∣α∣ の軌跡によって囲まれる部分の面積を求めよ。
→複素数分野:練習問題一覧|入試数学コンテスト過去問集
ド・モアブルの定理
正の整数 n と任意の実数 θ に対して,
(cosθ+isinθ)n=cosnθ+isinnθ
→ド・モアブルの定理の意味と証明
複素数平面における直線の方程式の一般形は,
az−az+b=0
(ただし,a
は任意の複素数で
b
は純虚数)
→複素数平面における直線の方程式
一次分数変換
a,b,c,d
を
ad=bc
なる複素数とする。複素数に対して複素数を返す関数で,
f(z)=cz+daz+b という形のものを一次分数変換(またはメビウス変換)という。
→一次分数変換(メビウス変換)と円円対応
東京大学理系数学2025年 第6問
複素数平面上の点 21 を中心とする半径 21 の円の周から原点を除いた曲線を C とする。
-
曲線 C 上の複素数 z に対し,z1 の実部は 1 であることを示せ。
-
α,β を曲線 C 上の相異なる複素数とするとき,α21+β21 とりうる範囲を複素数平面上に図示せよ。
-
γ を (2) で求めた範囲に属さない複素数とするとき,γ1 の実部がとりうる値の最大値と最小値を求め
よ。
→【解答・解説】東大理系数学2025 第6問
シムソンの定理

三角形
ABC
と点
D
がある。D
から直線
BC,CA,AB
に下ろした垂線の足を
P,Q,R
とおく。
このとき,D が三角形 ABC の外接円上にあるならば,P,Q,R は同一直線上にある。この直線をシムソン線と呼ぶ。
→シムソンの定理とその2通りの証明
問題
次の値を求めよ。
- 100C0+100C2+⋯+100C100
- 100C0+100C3+⋯+100C99
- 100C0+100C4+⋯+100C100
→飛び飛びの二項係数の和
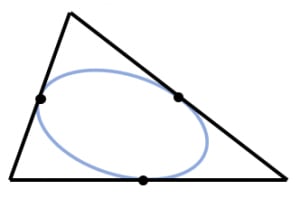
任意の三角形に対して,各辺と中点で接する楕円がただ一つ存在する。これをシュタイナーの(内接)楕円と呼ぶ。
→シュタイナーの内接楕円,Mardenの定理,Gauss–Lucasの定理







