数列 に関する39記事をまとめました。くわしくは各リンク先を見てください。
等比数列の和の公式
初項
a,公比
r,項数
n
の等比数列の和は(r=1
のもとで),
r−1a(rn−1)
→等比数列の和の公式(例題・証明・応用)
数列の極限は,
- (有限の値に)収束する
- 正の無限大に発散する/負の無限大に発散する
- 振動する
のいずれかである。2と3の場合をいずれも発散すると言う。
→数列の発散,収束,振動の意味と具体例
無限等比級数の公式
−1<r<1 のとき,
a+ar+ar2+⋯=1−ra
→無限等比級数の収束,発散の条件と証明など
等差数列
等差数列とは,同じ数ずつ増えていく(または減っていく)数の列のことです。
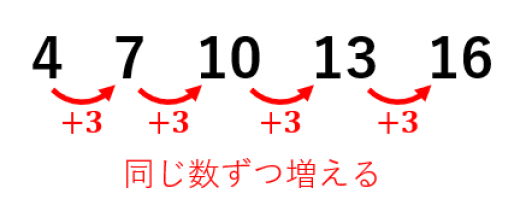
→等差数列の和
シグマ記号の公式
シグマ記号 Σ は「たくさんの足し算」を簡潔に表すための記号。シグマ記号に関連して,以下の公式が成立する:
k=1∑nak=1∑nkk=1∑nk2k=1∑nk3k=1∑nrk−1=na=21n(n+1)=61n(n+1)(2n+1)={21n(n+1)}2=1−r1−rn(r=1)
→シグマ記号の意味とその公式の応用例
逆数が等差数列である数列を調和数列と言う。例えば,
31,51,71,91,...
は逆数が 3,5,7,9,... となり等差数列なので,調和数列。
→調和数列
(1)平行移動の公式: i=1∑nai=i=k+1∑n+kai−k
→シグマ計算を機械的に行うための3つの公式
S1=t=1∑nt=21n(n+1)
S2=t=1∑nt2=61n(n+1)(2n+1)
S3=t=1∑nt3={21n(n+1)}2
S4=t=1∑nt4=301n(n+1)(2n+1)(3n2+3n−1)
S5=t=1∑nt5=121n2(n+1)2(2n2+2n−1)
→4乗の和,べき乗の和の公式
an+1=pan+f(n) は d 回階差を取ることによって上記の「f(n) が定数の場合」に帰着できる
→f(n)を含む二項間漸化式の2通りの解法
等差×等比の和
等差数列×等比数列 の和は,公比倍してから差を取ることで計算できる。
→等差×等比,2乗×等比の和を求める2通りの方法
k=1∑nak
を計算したいときに,ak=bk+1−bk
と分解できれば,途中の項が打ち消し合って
k=1∑nak=bn+1−b1
のように計算できる。
→望遠鏡和~部分分数分解など差に分解する4つの恒等式
利息計算に使う数のいろいろな表現
-
a
:元金,元本,初期段階で持っている金額,現在価値(PV)
-
r
:利息率,年利率,運用利率,利回り
-
n
:考える期間(単位は「年」とすることが多い),運用期間
-
b
:最終段階で持っている金額,将来価値(FV)
→複利法の意味と計算方法,具体例
階差数列
「次の数との差」を並べた数列のことを階差数列と言います。
例えば,1,2,5,10,17,26 という数列に対する階差数列は,
1,3,5,7,9 です。

→階差数列の意味と、もとの数列の一般項を求める方法
n
段のハノイの塔の最短手数は
2n−1
→ハノイの塔のルールと最短手数
分数で表された数列の和を計算する頻出問題を解説します。さらに,その問題を一般化してみます。
→分数で表された数列の和の問題と一般化
問題
1と2を合わせて n 個並べて,10進数で n 桁の整数を作ることを考える。
例えば n=3 のときは,111・112・121・122・211・212・221・222の8通りが考えられる。
(1) n=4 のとき,何通りの整数がありうるか求めよ。
(2) 偶数は何通りできるか n を用いて表せ。
(3) 3の倍数は何通りできるか n を用いて表せ。
(4) n≧2 のとき,最小の素因数が7以上である整数は何通りできるか n を用いて表せ。
ただし整数 N の素因数とは,N を割り切る素数のことを意味する。
→数列分野:練習問題一覧|入試数学コンテスト過去問集
フィボナッチ数列
フィボナッチ数列(fibonacci sequence)とは,
- 最初の2つは 1 で,
- 3つめ以降は「前の2つを足したもの」
になる数列のこと。つまり,
1,1,2,3,5,8,13,21,34,…

→フィボナッチ数列の8つの性質(一般項・黄金比・互いに素)
母関数
数列 an に対して,
f(x)=k=0∑∞akxk
を(数列 an の)母関数と呼ぶことがある。
→数列の母関数の意味とその応用例
三項間漸化式の特性方程式の解を
α,β
とおくと,漸化式の一般項は
an=Aαn+Bβn
と表される。A,B
は初期条件から求める。
→三項間漸化式の3通りの解き方
方針
漸化式
an+1=4an(1−an)
は,a1=sin2θ
と置くと倍角公式が出現してうまくいきます。知らないと厳しい問題です。
→ロジスティック写像と漸化式
漸化式の
an
や
an−1
の係数に
n
が含まれている場合,両辺に何かしらかけたり割ったりして
f(n+1)an+1
と
f(n)an
を作り出せばうまくいくことが多い
→階乗を用いる漸化式の解法
連分数
分数の分母にさらに分数が含まれている以下のような形のものを連分数と言います:
a0+a1+a2+a3+⋯b3b2b1
→連分数展開とその計算方法
→コッホ曲線の次元,曲線の長さなど
分数型漸化式の解き方
an+1=Can+DAan+B(C=0)
という漸化式は,
- B=0 なら逆数を取る
- B=0 なら平行移動して B=0 に帰着させる
と解ける。計算はそこそこ大変。
→一次分数型の漸化式の解法と例題
連立漸化式:
{an+1=Aan+Bbnbn+1=Can+Dbn
の解き方は3通り(以上)あります。
- どちらか消去して三項間漸化式に帰着
- {an+kbn} が等比数列になるように k を決める
- 行列で表して行列の n 乗を計算
→連立漸化式の3通りの解き方
シュトルツ=チェザロの定理
数列 {an},{bn} について,次のどちらかを満たすとする。
- {bn} は単調増加(もしくは単調減少)で n→∞limbn=±∞
- {bn} は単調増加(もしくは単調減少)で n→∞liman=n→∞limbn=0
このとき,極限 n→∞limbn−bn−1an−an−1 が存在すれば,
n→∞limbnan=n→∞limbn−bn−1an−an−1
である。
→シュトルツ=チェザロの定理~ロピタルの定理の数列版
この記事の概要
-
a1,a2,...,an の中で最大のものを求める問題では,akak+1 と 1 を比較するとよい。
-
(Ax+B)n を展開したときの xk の係数を ak とおく。ak を最大にするのは(多くの場合) k≒A+BAn のとき。
-
反復試行の確率の最大値(二項分布の最頻値)も2からわかる。
-
ak=nCk(nm)k(1−nm)n−k を最大にする k は k=m
→隣どうしの比と1を比較する(展開式の係数の最大・確率の最大値)
東京科学大学2025年 第4問
数列 {an} を
a1=a2=1an+2=an+1+an
により定め,数列 {bn} を
tanbn=an1
により定める。ただし,0<bn<2π とする。
(1) n≧2 に対して,an+1an−1−an2 を求めよ。
(2) m≧1(m は整数)に対して,a2m⋅tan(b2m+1+b2m+2) を求めよ。
(3) 無限級数 m=0∑∞b2m+1 を求めよ。
→フィボナッチ数列の逆数とタンジェント~東京科学大学2025第4問
東京大学理系数学2025年 第5問
n を 2 以上の整数とする。1 から n までの数字が書かれた札が各1枚ずつ合計 n 枚あり,横一列におかれている。1 以上 (n−1) 以下の整数 i に対して,次の操作 (Ti) を考える。
(Ti):左から i 番目の札の数字が,左から (i+1) 番目の札の数字よりも大きければ,これら2枚の札の位置を入れかえる。そうでなければ,札の位置をかえない。
最初の状態において札の数字は左から A1,A2,⋯,An であったとする。この状態から (n−1) 回の操作 (T1),(T2),⋯,(Tn−1) を順に行った後,続けて (n−1) 回の操作 (Tn−1),⋯,(T2),(T1) を順に行ったところ,札の数字は左から 1,2,⋯,n と小さい順に並んだ。以下の問いに答えよ。
- A1 と A2 のうち少なくとも一方は 2 以下であることを示せ。
- 最初の状態としてありうる札の数字の並び方 A1,A2,⋯,An の総数を cn とする。n が 4 以上の整数であるとき,cn を cn−1 と cn−2 を用いて表せ。
→【解答・解説】東大理系数学2025 第5問
x,f(x),f(f(x)),f(f(f(x)))⋯ のみの関数方程式は漸化式を用いると解けることがある
→漸化式を用いた関数方程式の解法
シルベスターの数列(Sylvester's sequence)
a0=2,an+1=an2−an+1
で定義される数列をシルベスターの数列と言う。
→シルベスターの数列とその性質
ソモスの数列
2
以上の自然数
k
に対して,
初期条件:
a0=a1=⋯=ak−1=1
および漸化式:
anan−k=i=1∑⌊k/2⌋an−ian−k+i
で定義される数列をソモスの数列という。
→ソモスの数列
ゼッケンドルフの定理(Zeckendorf's theorem):
任意の正の整数は「連続しない」フィボナッチ数の和で一意に表すことができる。
→ゼッケンドルフの定理とその証明
ファレイ数列とは
0 以上 1 以下であり,分母が n 以下であるような既約分数を小さい順に並べた数列を(n に対応する)ファレイ数列という。
→ファレイ数列の4つの性質とその証明
p0=3,p1=0,p2=2,
pn=pn−2+pn−3(n≧3)
によって定まる数列
pn
をペラン数列と言う。
→ペラン数列の一般項および素数との関係
円周上に
n
個の頂点を打ち,その全ての2頂点間を線分で結ぶ。このとき,円は
M
個の領域に分割されるとする。
M
の最大値は
an=241(n4−6n3+23n2−18n+24)
→モーザー数列
性質1
各項の各桁は
1,2,3
のいずれかである。
→Look-and-say sequence(見て言って数列)
- a0=a1=⋯=ak−2=0
- ak−1=1
- an=an−1+an−2+⋯+an−k(n≧k)
で定まる数列について考える。
→トリボナッチ数列、テトラナッチ数列とその一般項
群数列
ある規則にもとづいて区切られた(グループ分けされた)数列のことを群数列と呼ぶ。
例. 2,∣4,6,∣8,10,12,∣14,16,18,20,∣⋯
→群数列の問題と解き方のコツ








