整数 に関する87記事をまとめました。くわしくは各リンク先を見てください。
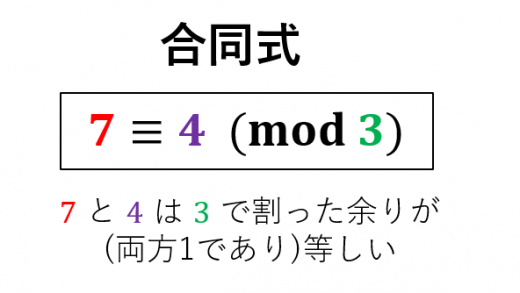
合同式
合同式とは,わり算の余りのみに着目した等式のこと。
→合同式(mod)の意味とよく使う6つの性質
約数の個数を求める公式
約数の個数は「素因数分解して」「それぞれの指数(右上の小さい数字)に1を足して」「全部かける」ことで計算できる。

→約数の個数の公式と平方数の性質
A=Nq+B のとき A が N の倍数 ⟺B が N の倍数
→倍数の判定法(2から12)とその証明一覧
この記事では,正の整数の約数の総和を計算する公式を解説します。入試でも頻出の必須公式です。

→約数の総和を求める二つの公式と証明
最大公約数と最小公倍数の関係
正の整数
a,b
に対して,それらの最大公約数を
g,最小公倍数を
l
とおくと
ab=gl
つまり,「最大公約数と最小公倍数の積」が「もとの二つの数の積」に等しい。
→最大公約数と最小公倍数の積の性質の2通りの証明
自然数について,以下の2通りの流儀があります:
- 自然数とは,正の整数のことである。
つまり,{1,2,3,...} のこと。
- 自然数とは,0以上の整数のことである。
つまり,{0,1,2,3,...} のこと。
→自然数とは(0を含むこともあるよ)
n進法とは,n種類の記号を用いて数を表現する方法。また,n進法で表された数をn進数という。
→n進法・n進数の解説と問題例
最大公約数とは
2つの正の整数について,両方ともを割り切る数(公約数)の中で一番大きいものを最大公約数と言います。
→最大公約数の4通りの求め方
定理1
x,y
に関する不定方程式
ax+by=c
が整数解を持つ
⟺c
は gcd(a,b)
の倍数
→一次不定方程式ax+by=cの整数解
平方剰余とは
「平方数を p で割った余りが a になる場合がある」とき,a は法 p で平方剰余であると言う。
→平方剰余と基本的な問題
- 十進法は,0,1,2,3,4,5,6,7,8,9,10,…
と数えていくお馴染みの方式。
- 二進法は,0,1,10,11,100,101,110,111,1000,…
と数えていく方式。
→二進法と十進法の変換方法と計算例
→互いに素の意味と関連する三つの定理
命題1(ゴールドバッハ予想)
2
より大きな偶数は2つの素数の和で表せる。
→ゴールドバッハ予想と関連する命題
エジプト分数
21 のように,分子が 1 である分数を単位分数と言います。
21+31+61 のように,分母が異なる単位分数の和のことをエジプト分数(エジプト式分数)と言います。
→エジプト分数(単位分数の和)に関する4つの話題
問題
正の整数 n に対し,n 以下で n と互いに素であるような正の整数の総和を S(n) とする。
例えば,S(1)=1,S(5)=1+2+3+4=10,S(6)=1+5=6 である。
以下の問いに答えよ。
(1) S(1024) を求めよ。
(2) m=20212021 とするとき,m2S(m) の値を求めよ。
(3) S(n) が偶数となるような 100 以下の正整数 n の総和を求めよ。
→整数分野:練習問題一覧|入試数学コンテスト過去問集
整数論の有名な定理
連続する n 個の整数の積は n! の倍数である。
→連続するn個の整数の積と二項係数
ルジャンドルの定理
n!
に含まれる素因数
p
の数は以下の式で計算できる:
i=1∑∞⌊pin⌋=⌊pn⌋+⌊p2n⌋+⌊p3n⌋+⋯
ただし,⌊x⌋
は
x
を超えない最大の整数を表す。
→ルジャンドルの定理(階乗が持つ素因数のべき数)
ピタゴラス数
ピタゴラス数 とは,a2+b2=c2 を満たす正の整数の組 (a,b,c) のこと。

→ピタゴラス数の求め方とその証明
重要な性質
割り算の等式:a=bq+r において,「a と b の最大公約数」=「b と r の最大公約数」
→ユークリッドの互除法の証明と不定方程式
定理
ある自然数
a
が存在して
an≡a(modn)
が成り立てば
n
は合成数。
→素因数分解の難しさと素数判定
整数
x
と
y
に関する不定方程式:
x2−Dy2=1
をペル方程式と言う。
→ペル方程式に関する基本的な性質まとめ
ガウス記号
実数 x に対して「x の整数部分」を ⌊x⌋ または [x] と書くことが多い。
ただし「x の整数部分」とは n≦x<n+1 を満たす整数 n のこと。
例えば,2.1 の整数部分は 2 なので ⌊2.1⌋=2
→ガウス記号の定義と3つの性質
A
と
B
が互いに素なとき,A
円の硬貨と
B
円の硬貨を使って支払えない金額の最大値は
(AB−A−B)={(A−1)(B−1)−1} 円。
→フロベニウスの硬貨交換問題
レイリー(Rayleigh)の定理
r1+s1=1
を満たす正の無理数
r,s
に対して以下が成立する。
全ての正の整数は以下の2つの数列のいずれかに必ず一回だけ登場する。
- ⌊mr⌋(m=1,2,3⋯)
- ⌊ns⌋(n=1,2,3⋯)
→レイリーの定理とその自然な証明
座標平面において,各成分が全て整数である点を格子点(こうしてん)と呼ぶ。
→格子点の個数を数える問題の5通りの解法
全ての桁が
1
である整数をレプユニット数と言う。
→レプユニット数
友愛数の定義
(自分自身を除いた)約数の総和=相手となる正の整数のペアのことを友愛数と呼ぶ。
→友愛数の意味と友愛数を生み出す公式
この記事のサマリ
- r が有理数なら,r の良い近似は有限個しかない
- r が無理数なら,r の良い近似が無限個ある
- r が無理数なら,連分数展開により r の良い近似が無限個得られる
→実数を分数で近似する【ディリクレのディオファントス近似定理】
定理1(整数値多項式の必要十分条件1)
P(x) を k 次多項式とする。
ある整数 n が存在して P(n),P(n+1),...,P(n+k) が整数なら,P(x) は整数値多項式
→整数値多項式の意味と2つの必要十分条件
定理
r が有理数であれば良い近似は有限個,r が無理数であれば良い近似は無限個ある。
→ディオファントス近似にまつわる入試問題
京都大学特色入試2024大問1
2 以上の自然数 n に対して,n を割り切る素数の個数を f(n) とする。例えば n=120 のとき,120 を割り切る素数は 2 と 3 と 5 なので,f(120)=3 である。不等式 f(n)≧2n を満たす 2 以上の自然数 n をすべて求めよ。
→素因数の数の評価~京大特色2024
ベンフォードの法則
多くの状況で自然数の最初の桁(最高位)に現れる数は一様に分布しない。
具体的に n (=1,2,…,9) の出てくる確率 Pn は
Pn=log10nn+1
に近いことが多い。
→ベンフォードの法則と京大数学2024
東北大学AO 2024
等式 x2+y2+z2−3xyz=0 を満たす正の整数の組は無限個あることを証明せよ。
→マルコフのディオファントス方程式~東北大AO入試を通して
問題(京都大学理系後期 1989)
2つの奇数 a,b に対して,m=11a+b,n=3a+b とおく。次の1,2を証明せよ。
- m と n の最大公約数は,a と b の最大公約数を d として,2d,4d,8d のいずれかである。
- m,n がともに平方数であることはない。
→ユークリッドの互除法と約数の考察~京大理系後期1989
京大特色2025 第1問
n を自然数とする。実数 x に対し,x を超えない最大の整数を [x] とし,f(x)=x−[x] と定める。このとき,1 よりも大きく,かつ整数でないような実数 x のうちで,
n→∞limf(nf(nx)1)=21
を満たすものをすべて求めよ。
→ガウス関数と極限の融合問題~京大特色2025第1問
一橋大学2025年第1問
正の整数 n に対し,n の正の約数の個数を d(n) とする。たとえば,6 の正の約数は 1,2,3,6 の4個なので
d(6)=4 である。また,
f(n)=nd(n)
とする。
(1) f(2025) を求めよ。
(2) 素数 p と正の整数 k の組で f(pk)≦f(pk+1) を満たすものを求めよ。
(3) f(n) の最大値と,そのときの n を求めよ。
→約数の個数の評価~一橋大学2025第1問
東京大学理系数学2025年 第4問
この問いでは,0 以上の整数の2乗になる数を平方数と呼ぶ。a を正の整数とし,fa(x)=x2+x−a とおく。
- n を正の整数とする。fa(n) が平方数ならば,n≦a であることを示せ。
- fa(n) が平方数となる正の整数 n の個数を Na とおく。次の条件 (i),(ii) が同値であることを示せ。
- (i) Na=1 である。
- (ii) 4a+1 は素数である。
→【解答・解説】東大理系数学2025 第4問
このページでは,無限降下法について解説します。
- 無限降下法とは何か?
- 無限降下法の簡単な応用例:3 が無理数であることの証明
- 無限降下法の難しい応用例:フェルマーの最終定理の n=4
→無限降下法の整数問題への応用例
オイラーのファイ関数
-
自然数
n
に対して,1
から
n
までの自然数の中で
n
と互いに素なものの数を ϕ(n) と書き,オイラーの ϕ 関数と呼ぶことがある。
-
ϕ 関数は
ϕ(n)=ni=1∏k(1−pi1)という式で計算できる。ただし,pi
は
n
の素因数。
→オイラーのファイ関数のイメージ
フェルマーの小定理
p が素数で,a が p の倍数でない正の整数のとき
ap−1≡1(modp)
→フェルマーの小定理の証明と例題
ソフィー・ジェルマン(Sophie Germain)の恒等式
a4+4b4=(a2+2ab+2b2)(a2−2ab+2b2)
→因数分解公式(ソフィージェルマンの恒等式)
0 以上の整数 n を用いて Fn=22n+1 と表される整数をフェルマー数と呼ぶ。

→フェルマー数とその性質
ウィルソン(Wilson)の定理
2 以上の整数 p について,p が素数 ⟺(p−1)!≡−1(modp)
→ウィルソンの定理とその2通りの証明
平方数でないことの証明には,以下の2つが有効な場合が多い。
- 平方剰余を考える
- 両側から1違いの平方数で挟む
→整数論のテクニック:平方数でないことの証明
中国剰余定理(二元の場合)
n1
と
n2
が互いに素なとき,
x≡a1(modn1)
x≡a2(modn2)
の両方を満たす整数
x
が
0
以上
n1n2
未満の範囲にただ1つ存在する。
→中国剰余定理の証明と例題(二元の場合)
中国剰余定理(一般の場合)
ni(i=1,⋯,k) たちがどの2つも互いに素なとき,k 本の連立合同式
x≡ai(modni)
を満たす x が 0≦x<n1n2⋯nk の範囲にただ1つ存在する。
→中国剰余定理と法が互いに素でない場合への拡張
原始根の定義
「3
以上の素数
p」 と「1
以上
p
未満の整数
r」
が以下の性質を満たすとき,r
を法
p
に対する原始根と呼ぶ。
「r,r2,…,rp−2 のいずれもが p で割って余り 1 でない」
(また,r=1
は
p=2
に対する原始根である,とする。)
→原始根の定義と具体例(高校生向け)
ルジャンドル記号
a
が
p
の平方剰余であるとき,
(pa)=1
と定義します。
また,a
が
p
の平方剰余でないとき,
(pa)=−1
と定義します。
→ルジャンドル記号とオイラーの規準
定理
2
つの整数
x,y
を用いて
n=x2+y2
と表される
⟺n
を素因数分解したときの
4k+3
型の素数の指数が全て偶数
→フェルマーの二平方和定理
Vieta jumping
Vieta jumping とは,ある文字について二次式であるような不定方程式を,解と係数の関係を用いて解くテクニックです。
→数オリのテクニック〜Vieta jumping〜
位数の性質
modp
における
a
の位数を
n
とする。
am≡1(modp) を満たすなら m は n の倍数である。
→位数の性質と原始根の応用
n
は正の整数,x,y
は任意の整数で,
p が奇素数で,x−y が p の倍数で,x と y が p の倍数でないとき,
vp(xn−yn)=vp(x−y)+vp(n)
→数オリの整数論(難問)に対するテクニック
→素数の間隔に最大値がないことの3通りの証明
平方剰余の相互法則(など)を用いることで,与えられた素数
pとp未満の非負整数aに対してp で割って a 余るような平方数が存在するか否かを素早く判定することができる。
→平方剰余の相互法則の意味と応用
ζn=en2πi=cosn2π+isinn2π
(n
乗して
1
になる数のうちの一つ)とおく。多項式
Fn(x)=k∈An∏(x−ζnk)
を円分多項式(円周等分多項式)と言う。
→円分多項式とその性質
フィボナッチ数列の余りの周期に関する定理
p
を素数とし,p=2,5
とする。
p
を
5
で割った余りが
1
または
4
なら,周期は
p−1
の約数
p
を
5
で割った余りが
2
または
3
なら,周期は
2(p+1)
の約数
→数列における余りの周期性(特にフィボナッチ数列)
素数が無限に存在することのいろいろな証明を紹介します。
→素数が無限にあることの4通りの証明
クロネッカーの稠密定理
任意の無理数
x
と
0≤a<b≤1
を満たす任意の実数
a,b
に対して
a≤{nx}≤b
を満たす自然数
n
が存在する。
→クロネッカーの稠密定理とその証明
完全数とは「約数の総和が自分の2倍になる」ような正の整数のことです。
→完全数の一覧と性質
素数の逆数和 21+31+51+71+⋯ は発散する。
→素数の逆数和が発散することの証明
1. Prime Number Theorem(素数定理)
1
から
n
までの整数の中にある素数の数を
π(n)
とおく。
n
が十分大きいとき,π(n)≒lognn
つまり,n→∞limnπ(n)logn=1
→整数論の美しい定理7つ
素因数分解の一意性
全ての正の整数は素数の積として(順番を除いて)一意に表せる。
→素因数分解の一意性とその証明について
リーマン予想
ゼータ関数の非自明な零点の実部は
21
である。
→リーマン予想の意味,素数分布との関係
エラトステネスの篩(ふるい)とは,n 以下の素数を全て見つけ出す高速な方法です。
→エラトステネスのふるいとその計算量
n
番目の三角数は
Tn=2n(n+1)
である。
→三角数とは,三角数定理,平方数との関係
素数一覧
5桁以下(10万以下)の素数を一覧にしました。番号つきです。全部で9592個あります。
→素数一覧(4桁以下,番号つき)
フェルマーの最終定理
n
を3以上の整数とするとき,xn+yn=zn
を満たす正の整数
x,y,z
の組は存在しない。
→フェルマーの最終定理
ロー法が成功したときには N の非自明な約数が得られている。
→素因数分解の高速なアルゴリズム(ロー法)
p,p+2 がいずれも素数であるときそれらを双子素数と言う。
→双子素数にまつわるいくつかの話題
→ナルシシスト数について
定理
2
以上の任意の整数
n
について,
d∣n∑μ(d)=0
→メビウスの反転公式の証明と応用
定理1
正
n
角形が定規とコンパスで作図可能
⟺
n=2Np1⋯pk
となる
0
以上の整数
N
と互いに異なるフェルマー素数
p1,⋯,pk
が存在する。
→正多角形の作図可能性の条件
Lucasの定理
任意の素数
p
と非負整数
m,n
に対して,
mCn≡i=0∏kmiCni(modp)
ただし,mkmk−1⋯m1m0
は
m
の
p
進数表示,nknk−1⋯n1n0
は
n
の
p
進数表示。
→Lucasの定理とその証明
クンマーの定理(Kummer's theorem)
mCn
が素数
p
で割り切れる回数は
m−n
と
n
を
p
進数表示して足し算をしたときの繰り上がりの回数と等しい。
→クンマーの定理とその証明
以下を満たす実数
r
をリウヴィル数(リュービル数)と言う:
任意の正の整数
n
に対して,ある正の整数
p,q(q≥2)
が存在して
0<∣∣r−qp∣∣<qn1
を満たす。
→リウヴィル数の具体例と性質
ガウス整数の定義
整数
a,b
を用いて
a+bi
と表される複素数をガウス整数(複素整数)と呼ぶ。
→ガウス整数とその応用
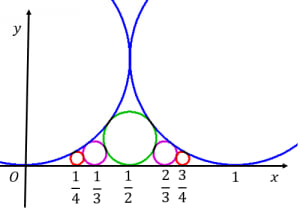
中心が
(pq,2p21)
で直径が
p21
である円を並べると美しい。
→フォードの円
3桁のカプレカ数は
495
のみである。
4桁のカプレカ数は
6174
のみである。
→カプレカ数(特に3桁の場合)について
定理
すべての原始ピタゴラス数は,⎝⎛345⎠⎞
に対して,3つの行列
A,B,C
のどれかをかける操作を何度か繰り返すことで作れる。ただし,
A=⎝⎛122−2−1−2223⎠⎞
,
B=⎝⎛122212223⎠⎞
,C=⎝⎛−1−2−2212223⎠⎞
→原始ピタゴラス数の木
ABC予想
a+b=c を満たす互いに素な自然数の組 (a,b,c) であって,任意の ϵ>0 に対して,
c>rad(abc)1+ϵ
を満たすものは有限個しか存在しない。
→ABC予想の主張の解説
チャンパーノウン定数(Champernowne Constant)
0. のあとに正の整数を 1 から小さい順に並べ続けた数
0.12345678910111213⋯
をチャンパーノウン定数と言う。
→チャンパーノウン定数
リュカ数(Lucas Number)
L0=2,L1=1,Ln=Ln−1+Ln−2(n≥2)
で定まる数列 {Ln} に現れる数をリュカ数と呼ぶ。
→リュカ数の意味とおもしろい性質~フィボナッチ数列の拡張
定理
任意の正の整数は1通りの階乗進数として表される。
→階乗進法,素数階乗進法,e進法
ラマヌジャンのタクシー数
1729 は2つの立方数の和として2通りに表される最小の自然数である:
1729=123+13=103+93
これを(ラマヌジャンの)タクシー数という。
→ラマヌジャンのタクシー数
定理1(ウォルステンホルムの定理)
5 以上の任意の素数 p に対して,
11+21+31+⋯+p−11
を既約分数で表したときの分子は p2 の倍数。
→ウォルステンホルムの定理
フェルマーの最終定理
n
を3以上の整数とするとき,xn+yn=zn
を満たす正の整数
x,y,z
の組は存在しない。
→フェルマーの最終定理の一般化
定理
q→1 で元の概念に一致するようにパラメーター q を追加した概念を q-類似という。
→q-二項係数とq-二項定理~東大数学2020年と合わせて











