n進法・n進数の解説と問題例

n進法は，n種類の記号を用いて数を表現する方法です。

• 例えば，10進法は $0,1,2,3,4,5,6,7,8,9$ という10種類の記号を用いて数を表現します。
• 2進法は $0,1$ という2種類の記号を用います。
• 16進法は $0,1,2,3,4,5,6,7,8,9$ に加えて $A,B,C,D,E,F$ という合わせて16種類の記号を用います。

n進法では，n個集まると繰り上がります。

• 例えば，10進法では $9$ の次が $10$ です。
• 2進法では $1$ の次が $10$ です。2集まると次のケタに繰り上がります。
• 16進法では $F$ の次が $10$ です。16集まると次のケタに繰り上がります。
• 4進法では $3$ の次が $10$ です。4集まると次のケタに繰り上がります。4進数と10進数の関係は下の表のようになります。

次に，n進法に関する「きちんとした式」を述べます。 n進法において，n個の記号のどれかを並べた $$a_k a_{k-1} a_{k-2} \cdots a_1 a_0 . a_{-1} a_{-2} \cdots a_{-m}$$ という記号列は $$a_k \times n^k + a_{k-1} \times n^{k-1} + a_{k-2}\times n^{k-2} + \cdots\\ +a_1 \times n + a_0 + \dfrac{a_{-1}}{n} + \dfrac{a_{-2}}{n^2} + \cdots + \dfrac{a_{-m}}{n^m}\\$$ という数を表すと定義します。定義は複雑でわかりにくいので，例を見てみましょう。

• 10進数で $403$ は $4\times 10^2+3$ のことを表します。
• 2進数で $1000$ は $1\times 2^3$ のことを表します。
• 4進数で $230.1$ は以下の数を表します：

$$\begin{aligned}　 &a_2 \times 4^2 + a_1 \times 4 + a_0 + \dfrac{a_{-1}}{4}\\ &= 2 \times 16 + 3 \times 4 + 0 + \dfrac{1}{4} \\ &= 32 + 12 + 0+ \dfrac{1}{4}\\ &= \dfrac{177}{4} \end{aligned}$$

また，n進数であることを明示したい場合は，数字の右下に小さく数字nを書きます。例えば，n進数の $2341$ は，$2341_{(n)}$ と表記します。

n進数は，ざっくり言えば下の位のものがn個集まると次の位に繰り上がる数の表現方法です。1円玉が10個集まると10円玉に，10円玉が10個集まると100円玉になるようなイメージです。

人間世界では10進法が主流ですが，必ず10を使わなければならないわけではありません。例えば，

• 時間の表現方法については60秒が1分，60分が1時間となるような60進法です。
• 週の数え方は7日で1週間なので7進法です。
• コンピュータの制御には0,1のみを用いた2進法が使われています。

n進法の考え方がなぜ必要なのでしょうか？

理由の1つは，n進法を使うことで，n種類の記号だけでいくらでも大きな数を表せるからです。

n進法を使わないで，「一億」までの数が表せるでしょうか？繰り上がりがないので，全ての数に一つの記号を対応させなければなりません。$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,\cdots, \%, !, ", \cdots$ などたくさん記号を持ってきて0から順に対応させるのは現実的ではないです。

つまり，大きな数を表すためには，規則を作って有限個の記号のみを使って表現することが必要です。

また，n進数は，各ケタを足したり引いたりすることが簡単にできます。つまり筆算ができる という特長もあります。

定義（さきほどのn進法の「きちんとした式」）により， $$1 \times 2^4 + 1 \times 2^2 + 1 = 21$$ と計算できます。 2進法と10進法を互いに変換するやり方については別の記事でもまとめています。→二進法と十進法の変換方法と計算例

定義により， $$3 \times 16^2 + 13 \times 16 + 10 + \dfrac{15}{16} + \dfrac{8}{16^2}\\ = \dfrac{31583}{32} = 986.96875$$ と計算できます。

このようにn進数を10進数で表すのは，定義に当てはめて計算するだけです。

10進数からn進数に変換する方法に与えられた数をひたすらnでわっていって，あまりを下から並べていくという方法があります。

例3の場合「$46$ から出発して $3$ で割った商 $15$ を下に，あまり $1$ を右下に書きます。出てきた商 $15$ に対して同じことを繰り返していきます。商が $0$ になった時点で終了します。最後に右側の列の数字を下から読むと答えになります。つまり， $$1201_{(3)}$$ が答えです。

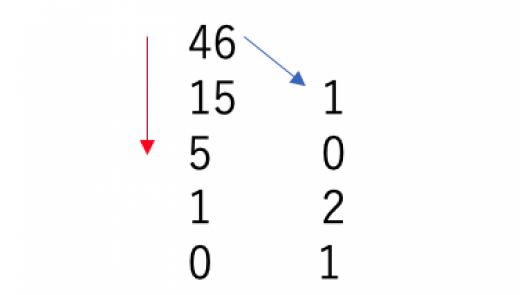
なぜこの方法でn進数に変換することができるのかは，二進法と十進法の変換方法と計算例で解説しています。

やや難しめの問題を考えてみます。

5桁で一番小さい3進数は $10000_{(3)}$ であり， 6桁で一番小さい3進数は $100000_{(3)}$ です。それぞれ10進数に変換すると， $$10000_{(3)} = 3^4 = 81\\ 100000_{(3)} = 3^5 = 243$$ となります。よって，$81$ 番目から $243-1=242$ 番目までが5桁です。その個数は $242-81+1=162$ 個です。

5桁で一番大きい3進数 $22222_{(3)}$ を考えても良いですが，計算が大変になります。上記の方法の方がスマートです。

求めたい5進数を $abc_{(5)}$ とおきます。問題の条件より $$abc_{(5)} \times 3 + 8 = abc_{(9)}$$ よって， $$3(25a + 5b + c) + 8 = 81a + 9b + c\\ 6a - 6b - 2c = 8\\ 3a - 3b -c = 4\\ 3a = 4 + 3b + c$$ ここで，$b,c \geq 0$ より， $$3a = 4 + 3b + c \geq 4$$ よって，$a \geq 2$ でなければならないことがわかります。そこで，$a=2,3,4$ の場合をそれぞれ考えます。

(i) $a = 2$ のとき $$3b + c = 2$$ $b > 0$ とするとこれを満たす $c$ は明らかに存在しなくなってしまうので，$b = 0$ よって，$c = 2$

(ii) $a = 3$ のとき $$3b + c = 5$$ $b > 1$ とするとこれを満たす $c$ は明らかに存在しなくなってしまうので，$b = 0,1$

$b = 0$ の時 $c = 5$ ですが，$a,b,c$ は5進数の記号であるため，$c \leq 4$ により不適です。

$b = 1$ の時 $c = 2$ は答えとして適します。

(iii) $a = 4$ のとき $$3b + c = 8$$ $b > 2$ とするとこれを満たす $c$ は明らかに存在しなくなってしまうので，$b = 0,1,2$

$b = 0$ の時 $c = 8$ ですが，$a,b,c$ は5進数の記号であるため，$c \leq 4$ により不適です。

$b = 1$ の時 $c = 5$ となって同様に不適です。

$b = 2$ の時 $c = 2$ となります。

(i),(ii),(iii)を全て合わせて，$202_{(5)}, 312_{(5)}, 422_{(5)}$ が答えとなります。

このように，n進法の考え方は整数問題の途中で登場することもあります。n進法の定義式を使って整数問題に持ち込む，という解き方の流れを再度確認しておきましょう。

Tag:数学Aの教科書に載っている公式の解説一覧