部分分数分解の3通りの方法
更新
部分分数分解とは, のように「いくつかの分数のたし算(または引き算)に分解する」こと。つまり,通分の逆。
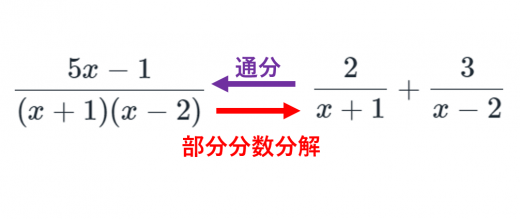
部分分数分解のやり方・例題・応用についてわかりやすく説明します。
部分分数分解の基本形と例題
部分分数分解の基本形と例題
うまいこと を選ぶと, となる。
公式1は覚えましょう。公式1を使って部分分数分解してみましょう。 を求める方法はいろいろあります。
を部分分数分解せよ。
例題1の解答を3通り紹介します。
方法1:係数比較
公式1より, と分解できる。両辺に をかけると,
これが恒等式となるので係数を比較して,
,
この連立方程式を解くと,,
つまり,答えは
このように,分母を払って係数を比較すると部分分数分解できます。 方法1は,部分分数分解のすべてのパターンに使える基本的な解法ですが,計算がややめんどうです。
方法2:数値代入
部分分数分解は,分母を払って数値を代入することでも計算できます。方法1ほどではありませんが,この方法も定番です。
分母を払うところまでは同じ:
ここで,
- を代入すると, より
- を代入すると, より
つまり,答えは
方法2も部分分数分解の全てのパターンに使えます。計算が少しめんどうですが,方法1よりは楽です。
方法3:裏ワザ
ヘビサイドの展開定理の定理2を使えば,係数を簡単に計算できます。覚える必要はないですが,おもしろいので興味がある方は上記の記事を読んでみてください。
に をかけて を代入すると となる。 をかけて を代入すると となる。よって,ヘビサイドの展開定理より
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題15では,部分分数分解で計算ミスをしないためのポイントも解説しています。
部分分数分解の簡単な問題
部分分数分解の簡単な問題
という単純な形なら,係数比較や数値代入をするまでもなく,直感で部分分数分解できます。
を部分分数分解せよ。
の分母に着目して,分数の引き算をつくってみる:
右辺の形を調節するために両辺を で割ると求める部分分数分解を得る。
もう少し複雑な形でも因数が2つならこの方法が使えます。
を部分分数分解せよ。
を部分分数分解すればよい。
分母に着目して分数の引き算をつくってみる(通分したときに分子の の項が消えるように調整):
両辺を 倍すると求める部分分数分解を得る:
この方法のメリット:
- 計算がとても楽
- 実戦で登場する多くの問題は方法3が使える形
この方法のデメリット:
- の形にしか使えない
部分分数分解の公式まとめ
部分分数分解の公式まとめ
部分分数分解をするためには,公式1に加えて,以下の公式2~4もおさえておくとよいです。
-
うまいこと を選ぶと,
-
うまいこと を選ぶと,
-
うまいこと を選ぶと,
-
うまいこと を選ぶと,
少し複雑に見えますが,両辺の分母の形を頑張って覚えましょう。 1と2を覚えれば3,4も覚えられます。より一般的な形はヘビサイドの展開定理の定理1をどうぞ。
ちなみに、部分分数分解は公務員試験など、大学受験以降でも利用する可能性があります。(参考:スキルアップ研究所)
この機会にしっかり覚えて、身につけていきましょう。
練習問題
練習問題
を部分分数分解せよ。
と分解できる(公式1)。分母を払うと
係数を比較すると
連立方程式を解くと, よって,答えは
を部分分数分解せよ。
と分解できる(公式3)。
分母を払うと,
がんばって展開して係数比較すると,
これを解くと,
分母を払うところまでは同じ:
を代入して,
これを解いて,
部分分数分解の応用例・例題
部分分数分解の応用例・例題
部分分数分解はいろいろな分野で使う基本的な計算です。応用例を紹介します。
部分分数展開による分数の和の計算
- 部分分数分解は,分数の和を計算するときに活躍します。
を求めよ。
であるから,
分数で表された数列の和の問題と一般化 でより詳しく解説しています。
積分計算への利用
- 積分計算でも役立ちます。
を求めよ。
であるから,
この他にも,三角関数の積分などにも用いられます。詳しくは 三角関数の有理式の積分 をご参照ください。
不等式の証明
不等式の証明で役立つこともあります。 こちらは微分を用いた不等式証明の問題で詳しく説明しています。
使える時には方法3(直感)を積極的に使って,使えない時は方法1と方法2のうちで自分の好きな方を使いましょう。











