積分 に関する70記事をまとめました。くわしくは各リンク先を見てください。
基準を x ではなく x−α にして積分すると楽な場合がある。
→置換積分を用いずに積分速度を上げる公式
1/6公式
∫αβ(x−α)(x−β)dx=−61(β−α)3
→放物線と直線で囲まれた面積を高速で求める1/6公式
積分公式を整理しました。基本公式から難問まで,すべて計算できれば積分マスターです!

→積分公式一覧
置換積分の公式(不定積分)
x=g(t) と置換すると,
∫f(x)dx=∫f(g(t))dtdxdt
→置換積分の公式の証明と例題
原始関数とは
微分すると
f(x)
になるような関数
F(x)
を
f(x)
の原始関数と言う。
→原始関数の定義といろいろな例
部分積分の公式

ただし,f′ は f の微分,G は g の積分(G′(x)=g(x))。
→部分積分の公式と覚え方,例題
(高校数学における)不定積分
微分すると f(x) になる関数(全体)のことを f(x) の不定積分と言う。
f(x) の不定積分を ∫f(x)dx と書く。

→不定積分の意味・公式・例題
定積分
∫abf(x)dx とは,F(b)−F(a) のことを表す。
ただし,F(x) は微分すると f(x) になる関数。
→定積分
∫eaxcosbx dx=a2+b2eax(acosbx+bsinbx)+C
∫eaxsinbx dx=a2+b2eax(asinbx−bcosbx)+C
→三角関数と指数関数の積の積分を一発で求める公式
定積分と面積
y=f(x) と x=a,x=b および x 軸で囲まれた部分の面積は,∫abf(x)dx という定積分で計算できる。
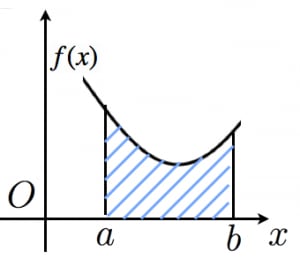
(ただし,a≦x≦b において f(x)≧0 とする)
→なぜ定積分で面積が求まるのか
瞬間部分積分
1:三列の表をつくる。二列目に上から
f(x),f′(x),f′′(x),⋯
と
0
になる手前まで格納する。
2:三列目に上から
g
の積分,g
の二階積分,⋯
と格納する。
3:一列目に上から
+,−,+⋯
と交互に格納する。
4:横にかけて縦に足す。
→瞬間部分積分のやり方と例題2問
対数関数の不定積分
∫logxdx=xlogx−x+C
→log xの積分計算の2通りの方法と発展形
∫tanxdx=−log∣cosx∣+C
∫tan2xdx=tanx−x+C
∫tannxdx=n−11tann−1x−∫tann−2xdx
→タンジェントとそのn乗の不定積分
指数関数の積分公式
∫exdx=ex+C
∫axdx=logaax+C
(ただし,a>0,a=1)
→指数関数(e^xとa^x)の積分と関連する公式
定積分で表された関数の微分の公式:
dxd∫axf(t)dt=f(x)
(ただし,f(t)
は
t
に関する1変数の関数)
→定積分で表された関数の微分の公式
回転体の体積公式

y=f(x),x=a,x=b,x
軸で囲まれた領域を
x
軸のまわりに回転させてできる図形の体積は,
V=∫abπ{f(x)}2dx
→回転体の体積を求める公式
区分求積法
区分求積法とは,「長方形の面積の和」で横幅を限りなく小さくしたものと y=f(x) の下側部分の面積が等しいという式:
n→∞limn1k=1∑nf(nk)=∫01f(x)dx

→区分求積法をわかりやすく【意味・例題・応用】
定数型の定石
定数型の積分方程式は,
∫abf(t)dt=k(=const.)
とおいて解くのが定石である。
→積分方程式の解き方
問題
O を原点とする xy 平面を考える。直線 x=1 上に点 A を取る。直線 OA の x≦0 の部分に AB=2 を満たす点 B が存在するとき, 以下の問いに答えよ。
(1) 直線 OA と x 軸がなす角を, x 軸の正方向から反時計回りを正として測って t(−2π≦t≦2π) とする。OB=r(r≧0) とするとき, r を t を用いて表せ。
(2) 点 A が直線 x=1 上をくまなく動くとき, 点 B の軌跡を C とする。曲線 C の y 座標の最大値を求めよ。
(3) 曲線 C によって囲まれる領域の面積を求めよ。
→微分・積分・極限分野:練習問題一覧|入試数学コンテスト過去問集
置換積分の公式(不定積分)
x=g(t) と置換すると,
∫f(x)dx=∫f(g(t))dtdxdt
である。
→置換積分で簡単になる計算例
置換積分の公式(不定積分)
x=g(t) と置換すると,
∫f(x)dx=∫f(g(t))dtdxdt
である。
→三角関数に関する置換積分3パターン
部分積分の公式
x=g(t) と置換すると,
∫f(x)dx=∫f(g(t))dtdxdt
である。
→部分積分で簡単になる計算例
シュワルツの不等式の積分バージョン
p≦x≦q で定義された任意の連続関数 f(x),g(x) に対して,
(∫pqf(x)2dx)(∫pqg(x)2dx)≥(∫pqf(x)g(x)dx)2
等号成立条件は
g(x)=tf(x)
となる
t
が存在する(または
f(x)=0 である)こと。
→シュワルツの不等式の積分形
ベータ関数の積分公式
m,n
が
0
以上の整数のとき,以下のような積分公式が成立する:
(i) 第一種オイラー積分
∫αβ(x−α)m(β−x)ndx=(m+n+1)!m!n!(β−α)m+n+1
(ii) 特に,α=0,β=1 とすると,
∫01xm(1−x)ndx=(m+n+1)!m!n!
→ベータ関数の積分公式
∫sinx1dx=21log(1+cosx1−cosx)+C
∫cosx1dx=21log(1−sinx1+sinx)+C
→1/sinx(サイン分の1)と1/cosx(コサイン分の1)の積分
ウォリス積分
∫02πsinnxdx=∫02πcosnxdx=⎩⎨⎧n!!(n−1)!!n!!(n−1)!!2π(nが奇数)(nが偶数)
→ウォリス積分~sinのn乗,cosのn乗の積分公式
公式1:∫x2+a2dx=log(x+x2+a2)
公式2:∫x2+a2dx=21(xx2+a2+a2log(x+x2+a2))
→ルートx^2+a^2の積分計算の2通りの方法
ヤングの不等式(Young's inequality)
a,b>0,p,q>1,p1+q1=1
のとき,
pap+qbq≥ab
等号成立条件は ap=bq
→ヤングの不等式の3通りの証明
King Property
∫abf(x)dx=∫abf(a+b−x)dx
→対称性を用いた定積分の計算(King Property)
ガウス積分
ガウス積分とは,以下のような定積分のことです。
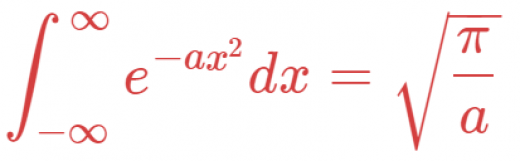
→ガウス積分の公式の2通りの証明
三角関数の積の積分は,積和公式で和にすることで計算できる。
→三角関数の積の積分と直交性

r(θ)
が連続関数のとき,極方程式
r=r(θ)
で表される曲線と
θ=α,β
で囲まれる部分の面積は,∫αβ21r(θ)2dθ で表される。
→極方程式の面積公式と例題
バームクーヘン積分(バウムクーヘン分割)

連続関数
y=f(x),x
軸,x=α,x=β
(ただし
0≦α<β)で囲まれた図形を
y
軸の回りに回転させてできる立体の体積
V
は,
V=∫αβ2πx∣f(x)∣dx
となる。
→バームクーヘン積分の例と証明
パップスギュルダンの定理
面積が
S
である平面図形
A
がある。A
を直線
l
の回りに回転させてできる回転体の体積
V
は,
V=2πgxS=(重心の移動距離) ×S
(gx
は重心と回転軸の距離)
ただし,A
を回転させる過程で
A
自身とは重ならないとする。
→パップスギュルダンの定理とその証明
傘型分割(傘型積分)
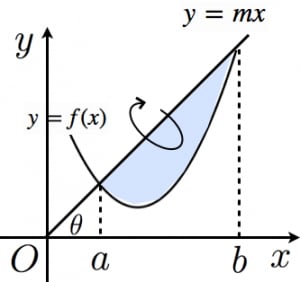
図のように,直線 l:y=mx と曲線 y=f(x) で囲まれた部分を l の回りに回転させてできる図形の体積は,
πcosθ∫ab{mx−f(x)}2dx
ただし,θ
は
l
と
x
軸のなす角で,m=tanθ
→傘型分割(傘型積分)と斜回転体の体積
ガウスグリーンの定理
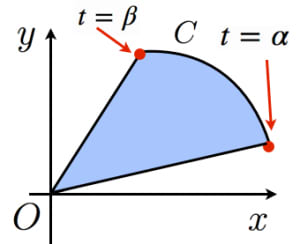
x=x(t),y=y(t)
と媒介変数表示された曲線
C
がある。
α≤t≤β
の範囲で
t
の増加とともに
(x(t),y(t))
が原点中心に反時計回りに動くとき,動径が掃いた部分の面積は,
S=∫αβ21(xy′−yx′)dt
→ガウスグリーンの定理の入試への応用
曲線の長さ(普通の関数版)
y=f(x)
で表される曲線の
a≤x≤b
の部分の長さは,
∫ab1+f′(x)2dx
(ただし,f(x) は微分可能で f′(x) は連続とする)
→曲線の長さを計算する積分公式(弧長積分)
台形公式を使うことで定積分の近似値を求めることができる。
→台形公式を用いた積分の近似とその誤差
- 有理式(有理関数・分数関数)の不定積分は必ず計算できる。
- 三角関数の有理式の積分は tan2x=t と置換することによって必ず計算できる。
→三角関数の有理式の積分

極座標平面において,図のように
θ=α,θ=β,r=r(θ)
で囲まれた,x
軸の上側にある図形を
D
とする。
D
を
x
軸(始線)の回りに回転させてできる立体の体積は,
32π∫αβr(θ)3sinθdθ
→極座標における回転体の体積公式
サイクロイドと面積・体積・長さ
サイクロイド曲線 C:
{x=a(θ−sinθ)y=a(1−cosθ)
(a>0,0≦θ≦2π)について,
- C と x 軸で囲まれた部分の面積は 3πa2
- x 軸周りの回転体の体積は 5π2a3
- 長さは 8a
→サイクロイド曲線のグラフと面積・体積・長さ
考える図形
 半径 r の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を R(≥r) とする。
半径 r の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を R(≥r) とする。
→ドーナツ(トーラス体・円環体)の体積・表面積を2通りの方法で計算
東大理系数学2019 第一問
次の定積分を求めよ。
∫01(x2+1+x2x)(1+(1+x2)1+x2x)dx
→【解説】東大理系数学2019 第一問
オイラーの定数
γ=n→∞lim(k=1∑nk1−logn)
をオイラーの定数(オイラー・マスケローニ定数)といいます。
→オイラーの定数γの意味と東大の過去問
定理
π を円周率とする。正の整数 n に対し
anbn=∫02−31+x21−x4ndx=∫02−31+x21+x4n+2dx
とおく。
- n→∞liman=n→∞limbn=12π を示せ。
- 3.141<π<3.142を証明せよ。ただし
1.7320508<3<1.7320509
である。
→arctan のマクローリン展開を用いた円周率の計算~大阪大学挑戦枠2013
東京大学理系数学2025年 第2問
-
ⅹ>0 のとき,不等式 logx≦x−1 を示せ。
-
次の極限を求めよ。
n→∞limn∫12log(21+xn1)dx
→【解答・解説】東大理系数学2025 第2問
東京大学理系数学2025年 第1問
座標平面上の点 A(0,0),B(0,1),C(1,1),D(1,0) を考える。実数 0<t<1 に対して,線分 AB,BC,CD を t:(1−t) に内分する点をそれぞれ Pt,Qt,Rt とし,線分 PtQt,QtRt を t:(1−t) に内分する点をそれぞれ St,Tt とする。さらに線分 StTt を t:(1−t) に内分する点を Ut とする。
- 点 Ut の座標を求めよ。
- t が 0≦t≦1 の範囲を動くときに点 Ut が描く曲線と,線分 AD で囲まれた部分の面積を求めよ。
- a を 0<a<1 を満たす実数とする。t が 0≦t≦a の範囲を動くときに点 Ut が描く曲線の長さを,a の多項式の形で求めよ。
→【解答・解説】東大理系数学2025 第1問~ベジェ曲線
底面の半径が
r1,天面の半径が
r2,高さが
h
である球台の体積は,
V=61πh(3r12+3r22+h2)
→球欠,球台の体積と球冠,球帯の表面積
ボールウェイン積分
0
以上の整数
n
と,k=1∑n∣ak∣≤1
を満たす実数
a1,⋯,an
に対して,
∫0∞xsinx(k=1∏nakxsinakx)dx=2π
→ボールウェイン積分
Sophomore's dream
(1)
∫01xx1dx=n=1∑∞nn1
(2)
∫01xxdx=−n=1∑∞(−n)−n
→2年生の夢(sophomore's dream)
ルジャンドル多項式
Pn(x)=2nn!1dxndn(x2−1)n
と表される多項式系をルジャンドル多項式という。
→ルジャンドル多項式の性質と計算
1
と
2
の算術幾何平均
M(1,2)
は,単位円周の長さ
l=2π
とレムニスケートの長さ
L
の比に等しい:
M(1,2)=Ll
→算術幾何平均とレムニスケートの長さ
オイラー・マクローリンの和公式(Euler–Maclaurin formula)
任意の正の整数 m,n に対して,
x=1∑nf(x)−∫0nf(x)dx=21{f(n)−f(0)}+k=1∑m(2k)!b2k{f(2k−1)(n)−f(2k−1)(0)}−(2m)!1∫0nB2m(x−⌊x⌋)f(2m)(x)dx
ただし,f(x) は 0≤x≤n において C2m 級である関数。
→オイラー・マクローリンの和公式
楕円積分(ルジャンドルの標準形)
-
E(k,ϕ)=∫0ϕ1−k2sin2θdθ
のことを第二種楕円積分という。
-
F(k,ϕ)=∫0ϕ1−k2sin2θ1dθ
のことを第一種楕円積分という。
→楕円積分の意味と身近な4つの例
台形公式
∫abf(x)dx≒2(b−a)f(a)+2(b−a)f(b)
特に,f(x) が1次以下の多項式なら両辺は等しい。
→ガウス求積法(Gauss–Legendre 公式)
掛け算の形の極限は log を取ることで計算できることがある。
→log × 区分求積
n
次元単位超球の体積は,
Vn=Γ(2n+1)π2n
→n次元超球の体積の求め方と考察
∫0∞ex−1x3dx=15π4
→x^3/e^x-1の定積分
任意の(なめらかな)関数 f(x) に対して
∫−∞∞f(x)δ(x)dx=f(0)
を満たすような「仮想的な」関数 δ(x) を,ディラック(Dirac)のデルタ関数という。
→ディラックのデルタ関数
-
b→∞lim∫abf(x)dx のことを,∫a∞f(x)dx と書くことがある。
-
a→−∞lim∫abf(x)dx のことを,∫−∞bf(x)dx と書くことがある。
→広義積分の意味といろいろな例
コーシーの積分公式(コーシーの積分表示)
- D を単純閉曲線(自分と交わらない閉じた曲線)で囲まれた領域とする。
- f を領域 D=D∪∂D で正則な関数とする。
このとき D の内部の任意の点 z で
f(z)=2πi1∮∂Dζ−zf(ζ)dζ
となる(線積分の向きは反時計回り,より厳密には領域の内側から見て左周りに定める)。
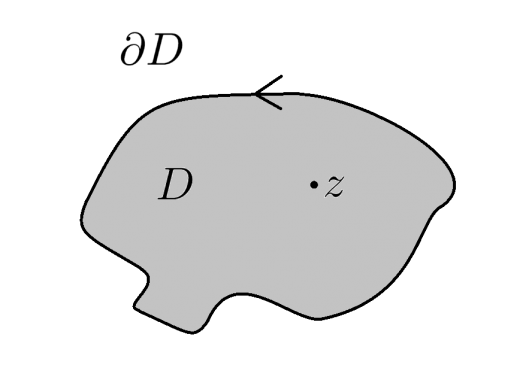
→コーシーの積分公式とその応用~グルサの定理・モレラの定理
重積分の変数変換
2変数 x,y を2変数 u,v に変換する。
このとき xy 平面上の領域 D が uv 平面上の領域 E に一対一に対応するとき,D 上の積分可能関数 f の重積分は次のように計算される。
∬Df(x,y)dxdy=∬Ef(x(u,v),y(u,v))∣detJ∣dudv
ただし ∣detJ∣ はヤコビ行列
J=⎝⎛∂u∂xdu∂y∂v∂x∂v∂y⎠⎞
の行列式(ヤコビアン)の絶対値である。
なお,n 変数のときも同様に計算される。
→重積分の変数変換とヤコビアン
バーゼル問題
n=1∑∞n21=6π2
→重積分を用いたバーゼル問題の美しい証明
逐次積分できる条件
f が [a,b]×[c,d] 上で
- 可積分な連続関数
- 非負な連続関数
のいずれかを満たすなら,以下の式が成り立つ。
∫ab(∫cdf(x,y)dy)dx=∫[a,b]×[c,d]f(x,y)dxdy=∫cd(∫abf(x,y)dx)dy
つまり逐次積分と重積分は一致する(積分の順序を交換できる)。
- また,いずれかの順序での(絶対値の)積分値が有限の値になれば,積分の順序を入れ替えてよい。
- また,有界な閉領域上での連続関数の重積分の順序は入れ替えてよい。
→フビニの定理~重積分の計算について
定理
関数 f(x) が f(x)=n=0∑∞anxn と無限級数展開されているとする。
この級数の収束半径を r とすると,∣x∣<r のもとで項別微分・項別積分ができる:
f′(x)∫f(x)dx=n=1∑∞nanxn−1=n=0∑∞n+1anxn+1+C
→項別微分・項別積分
∫x4+1dx=421{log(x2+2x+1)−log(x2−2x+1)+2arctan(2x+1)−2arctan(1−2x)}
→1/(x^4+1) の積分
問題(東大数学科院試 2021より)
p>21 に対して,次の値を求めよ。
Γ(2p1)1∫0∞xsin(xp)dx
ただし,正の実数 x に対して,Γ(x) は次式で与えられるものとする。
Γ(x)=∫0∞tx−1e−tdt
→三角関数と無理関数の合わさった積分(東大院2021より)
定義
関数 f(x) に対して
L[f](s)=∫0∞e−sxf(x)dx
という「s についての関数を返す変換」をラプラス変換という。
→ラプラス変換の定義と具体例・性質
定理
ベータ関数とは,p,q>0 に対して
B(p,q)=∫01xp−1(1−x)q−1dx
と定義される(広義)積分である。
→ベータ関数の基本的な性質~ガンマ関数との関係・広義積分の収束
ビュフォンの針
平面上に間隔 d で平行線を引く。長さ l(≦d) の針を適当に投げたとき,針が線と交わる確率は πd2l

→ビュフォンの針の問題と確率の導出






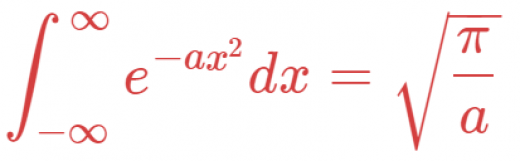





 半径 の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を とする。
半径 の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を とする。






