ディラックのデルタ関数

デルタ関数は関数 $f(x)$ と掛け算して積分したときに $x=0$ での値を取り出すような関数です： $$\int_{-\infty}^\infty f(x)\delta(x)dx=f(0)$$

しかし，普通の意味の関数でこの性質を持つものは存在しません。あくまで関数から $x=0$ での値を取り出す操作 $$f \mapsto f(0)$$ を積分で無理矢理あらわすための「仮想的な」関数がデルタ関数です。よって，デルタ関数とは関数というよりも「便利な記号」のようなもので，積分して初めて意味をもつものです（$dx$ のような記号に近い存在かもしれません）。

しかし，普通の関数ではないといっても直感的なイメージを持っておくことは大切です。そこで，デルタ関数を普通の関数で近似することを考えてみましょう。

任意の $f(x)$ について

$$\int_{-\infty}^\infty f(x)\delta(x)dx=f(0)$$

を満たす $\delta(x)$ は，直感的には下図のような

$x=0$ の非常に近くのみで大きい値となる関数

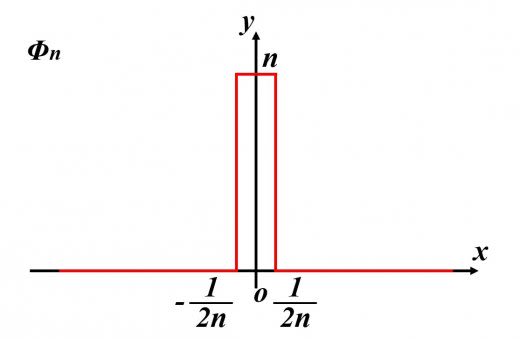
と考えられます。この関数を $\phi_n(x)$ としましょう。もちろんこれは厳密なデルタ関数ではありません。例えば $f(x)=x^2$ としてみると

$$\begin{aligned} \int_{-\infty}^\infty f(x)\phi_n(x)dx &= \int_{-\frac{1}{2n}}^{\frac{1}{2n}} nx^2 dx\\ &= n\left[\frac{x^3}{3} \right]_{-\frac{1}{2n}}^{\frac{1}{2n}}\\ &=\frac{1}{12n^2} \end{aligned}$$ なので，$f(0)=0$ とは少しずれてしまいます。しかし，$n \to \infty$ の極限をとればきちんと $0$ に収束します。さらに他の $f(x)$ でも同じことが成立します。

定理1により，$\phi_n(x)$ は $n \to \infty$ の極限においてデルタ関数 $\delta(x)$ をあらわすとみなせそうです。さらに，この定理が成り立つことから，記号を濫用して $$\lim_{n \to \infty} \phi_n(x)=\delta(x)$$ と書いたりもします。この極限は普通の意味の極限ではないことに注意しましょう！

このように，デルタ関数は関数ではないですが，普通の関数によってある意味で近似できます。また，この $\phi_n(x)$ 以外にも定理1の条件を満たす関数列はたくさんあります。いくつか例をあげておきます。

デルタ関数は関数ではなく積分して初めて意味のある記号ですが，例えば$$\delta'(x) = -\delta(x)\frac{d}{dx}$$$$x\delta(x)=0$$のような式を目にすることもあります。これは $f(x)$ をかけて積分した後の式において等式が成り立つ，という意味です。このような等式や性質をいくつか紹介します。

形式的な表示

デルタ関数の積分では $x \neq 0$ の部分の影響がなくなります。ここから $\delta (x)$ は $x \neq 0$ で $0$ を取ると考えられます。

$f(x) = 1$ に対してデルタ関数の積分をすると $$\int_{-\infty}^{\infty} \delta (x) dx = 0$$ です。

これより $\delta (0) = \infty$ であると（形式的に）考えるとよいです。

このことを踏まえると，正の実数 $a,b$ に対して $$\int_{-a}^b f(x) \delta (x) dx = f(0)$$ となります。

変数変換

$a\neq 0$ に対して$$\delta(ax) = \frac{1}{|a|}\delta(x)$$が成り立ちます。これは $ax=y$ による置換積分からわかります。実際，$a>0$ のとき， $$\begin{align*} \int_{-\infty}^\infty f(x)\delta(ax)dx&=\frac{1}{a}\int_{-\infty}^\infty f\left(\frac{y}{a} \right)\delta(y)dy\\ &=\frac{1}{a}f\left(\frac{0}{a}\right)\\ &=\frac{1}{a}f(0) \end{align*}$$ となります。$a < 0$ のときは置換した際に積分区間が逆転してマイナスがつくので $-\dfrac{1}{a}f(0)$ になります。

微分

デルタ関数の微分は$$\delta'(x) = -\delta(x)\frac{d}{dx}$$を満たします。

これは（$\lim _{x \to \pm \infty}f(x)=0$ となる $f(x)$ について）部分積分によって $$\begin{align*} \int_{-\infty}^\infty f(x)\delta'(x)dx&=\Bigl[f(x)\delta(x)\Bigr]_{-\infty}^{\infty}-\int_{-\infty}^\infty f'(x)\delta(x)dx\\ &=-f'(0) \end{align*}$$ が成り立つ，という意味です。

平行移動

デルタ関数を平行移動した $\delta(x-a)$ は，$x=a$ での値を取り出す操作を表します。 $$\int_{-\infty}^\infty f(x)\delta(x-a)dx=f(a)$$ （$y=x-a$ として置換積分すればわかります。）これは物理などで「位置 $a$ にある電荷」などをあらわすときに使われます。

フーリエ級数展開

デルタ関数を周期 $T$ になるように拡張して関数を考えます。（記号の乱用ですが $\delta (x)$ と書きましょう）

これをフーリエ級数展開してみましょう。

$$\begin{aligned} a_n &= \dfrac{2}{T} \int_0^{T} \delta (x) \cos\dfrac{2\pi nx}{T}dx\\ &= \dfrac{2}{T}\\ b_n &= \dfrac{2}{T} \int_0^{T} \delta (x) \sin\dfrac{2\pi nx}{T}dx\\ &= 0 \end{aligned}$$

よって $$\delta (x) = \dfrac{1}{T} + \sum_{n=1}^{\infty} \dfrac{2}{T} \cos 2\pi n x$$ となります。

複素数型フーリエ級数展開もしてみましょう。

$$\begin{aligned} \delta &= \dfrac{1}{T} e^{\frac{2 \pi}{T} \cdot 0 \cdot x} + \sum_{n=1}^{\infty} \dfrac{1}{T} (e^{\frac{2 \pi}{T} n x} + e^{-\frac{2 \pi}{T} n x})\\ &= \dfrac{1}{T} \sum_{n=-\infty}^{\infty} e^{\frac{2 \pi nx}{T}} \end{aligned}$$ となります。この表記は計算する上で有用です。

フーリエ変換

デルタ関数をフーリエ変換（→フーリエ変換の意味と応用例）すると， $$\begin{aligned} \hat{\delta} (\xi) &= \int_{-\infty}^\infty \delta(x)e^{i\xi x}dx\\&=e^0\\&=1 \end{aligned}$$ となり，定数関数 $1$ となります。さらにこれをフーリエ逆変換すると$$\delta(x) = \frac{1}{2 \pi}\int_{-\infty}^\infty e^{ikx}dk$$という式が得られます。これは数学的にはかなり怪しい式変形ですが，物理学では利用されるようです。また右辺の積分を有限区間で打ち切ると $$\begin{aligned} \frac{1}{2 \pi}\int_{-n}^n e^{ikx}dk &= \Bigl[\frac{e^{ikx}}{ix}\Bigr]_{-n}^n\\ &=\frac{1}{2 \pi}\left(\frac{e^{inx}}{ix}-\frac{e^{-inx}}{ix}\right)\\ &=\frac{1}{2 \pi}\frac{e^{inx}-e^{-inx}}{ix}\\ &=\frac{1}{2 \pi}\frac{2i\sin n x}{ix}\\ &=\frac{\sin n x}{\pi x} \end{aligned}$$ となり，「デルタ関数の近似列」のひとつとしてあげた $\varphi_n(x)$ が現れます。

デルタ関数のような「関数に対し値を返す線形な関数」は，超関数と呼ばれます。初めに物理や工学でデルタ関数や階段関数を使った（数学的にちょっと怪しい）計算が導入され，それを正当化するためにローラン・シュワルツによって超関数（distribution）の理論として整理された，という歴史があります。

上のような計算をどうやって厳密化するのか，といったことに興味がある方は超関数や関数解析について調べてみてはいかがでしょうか。