高校数学の美しい物語
更新
当サイトには1000以上の記事があります。
高校数学の教科書レベルから大学院レベルの難しいものまで,基本的にはすべての記事が独立しているので,好きなものから読んでください。
おすすめの新着記事
おすすめの新着記事
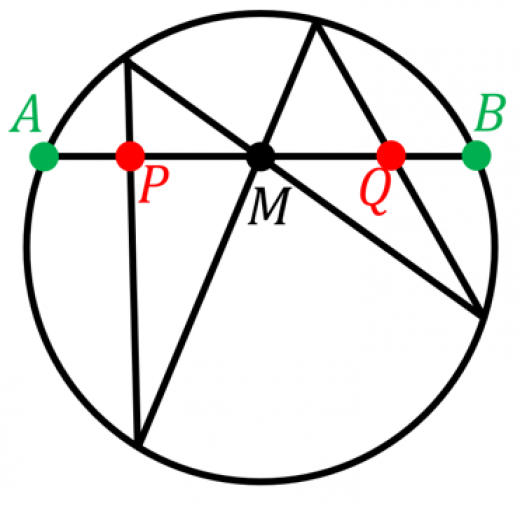
胡蝶定理
ハーディの不等式・カールマンの不等式
この記事では,カールマンの不等式の証明を目標に,おもしろい不等式を紹介していきます。
カールマンの不等式(Carleman's inequality)
非負の数 について,
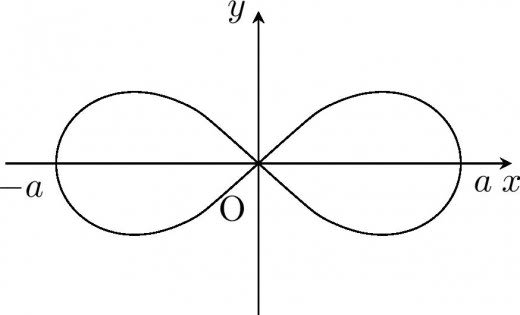
レムニスケート
定義
レムニスケート曲線とは,極方程式 で表される曲線である。
おすすめの人気記事
おすすめの人気記事
ミレニアム懸賞問題
ミレニアム懸賞問題の概要,一覧,そしてそのうちのいくつかについての大雑把な説明をします。
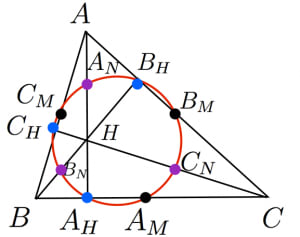
九点円の定理
あみだくじの確率
あみだくじの確率には,かなりの偏りがある。
半正多面体と準正多面体
- 半正多面体と準正多面体の意味を説明します。
- 半正多面体全13種類を紹介します。
- 13種類しかないことを証明します。