東大文系数学2020入試過去問解答解説
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2020年度入学試験の文系数学について解説します。
第一問[微分]
第一問[微分]
とする。座標平面上の曲線 が以下の2条件を満たすとする。
条件1: は 軸に接する。
条件2: 軸と で囲まれた領域(境界は含まない)に, 座標と 座標がともに整数である点がちょうど1個ある。
を で表し, のとりうる値の範囲を求めよ。
第一問です。この問題には小問がなく誘導がないので,自分で戦略を立てなければなりません。
微分してグラフの概形を書くと, で極値を取ることがわかります。 の方の極値は であり,条件より必ず正です。条件1として は 軸に接しなければなりませんから, における極値 が成立すればよいです。
条件2がとても考えづらいですね。どうすれば良いでしょうか。
整数の問題では,必要条件から値を絞るということをよく考えると思います。それと同じように考えます。つまり,「条件2を満たすための必要条件を考え,その十分性を確認する」という流れで解答をつくります。よくわからないかもしれないので具体的にみていきましょう。
における曲線上の点の 座標は,条件1より であることが求められます。 がもし より大きかったとすると, 軸と で囲まれた領域に という二点を含んでしまいことになり,条件2が成立しませんので, が必要です。
また, がもし 以下だとすると, 座標と 座標がともに整数である点が存在しないことが少しの議論の後にわかります。よって が必要です。
ここで のとき, 以外に 座標と 座標がともに整数である点は存在しないことを示すことができます。よってこの条件が必要かつ十分な条件であることになります。
解答が少し書きづらい問題だと思いますが,このような論理の流れを全面に押し出した解答例を以下に示してみたいと思います。
とする。 より, の増減表は以下のようになる。
ここで条件1は, であることを考えると,
と同値である。このとき
であり, のグラフは以下のようになる。

条件2について考える。 のとき 軸と で囲まれた領域には という二点が含まれ,条件2が成立しない。よって条件2が満たされるには が必要である。
また, のとき, において であるから, 軸と で囲まれた領域には 座標と 座標がともに整数である点は存在しない。よって条件2が満たされるには が必要である。
まとめると, つまり が必要である。この必要条件が条件2の十分条件でもあることを確認する。
と, により, 座標と 座標がともに整数である点は 上か 上に限られる。 と の大小関係を考える。 ここで より したがって であるから 上には 座標と 座標がともに整数である点は存在しない。
上には 座標と 座標がともに整数である点が ただ一点のみ存在するから,条件2の必要十分条件は であることが確かめられた。
ちなみに,最初からうまく必要かつ十分な条件をすんなりと見つけられる訳ではありません。試行錯誤の結果,十分性が保証される必要条件がみつかって初めて答えとして採用できています。整数の分野において,必要条件の見つけ方は問題によって異なるように,問題に合わせてうまくやれる方法を探す必要があります。
第二問[場合の数]
第二問[場合の数]
座標平面上に8本の直線 がある。以下,16個の点 から異なる5個の点を選ぶことを考える。
(1) 次の条件を満たす5個の点の選び方は何通りあるか。
上の8本の直線のうち,選んだ点を1個も含まないものがちょうど2本ある。
(2) 次の条件を満たす5個の点の選び方は何通りあるか。
上の8本の直線は,いずれも選んだ点を少なくとも1個含む。
設定はシンプルな問題ですが,第一問よりもさらに論述を書くのがとても大変な問題です。また,場合分けを正確にできないと数え間違いを起こしてしまいます。着実に丁寧にときましょう。
まず(1)ですが,選んだ点が一個も含まれない直線が,縦なのか横なのかで場合分けします(以下の議論は紙面上で図を書きながら追いかけることを推奨します)。
最初に縦の場合として,例えば, の直線上には点が一個も含まれない状況を考えます。すると, と は少なくとも一個以上の点を含まなければなりません。
ここで, に何個ずつ点を配分すれば良いかを考えます。全部で 個になるはずですから, 本の直線のうち, 本だけが 個点を含み,そのほかの 本には点が つのみ含まれることになります。 に点が 個含まれるとしましょう。 には点が含まれないので, に点があることが確定します。
これにより に少なくとも点が一個以上あることが保証されたので,残りの三点について, のどちらか, のどちらか, のどちらかの 通りの選び方がありますから,これまでの議論をまとめると縦の場合の総数が求められます。
上記のように,具体的にあてはめながら解くのがこの問題では得策でしょう。ただし具体的に当てはめて解く際は,そのように仮定しても一般性を失わないかどうかきちんと考えるようにしましょう。
(i)選んだ点を 個も含まない直線が であるとき
の選び方は 通りある。ここでは の状況を考える。このとき と には少なくとも点を 個含む。
ここで, に何個ずつ点が含まれるかを考える。これらは少なくとも 個の点を含むので, 本の直線のうち, 本だけが 個点を含み,そのほかの 本には点が 個のみ含まれる。 個点を含む直線を とする。 の選び方は 通りである。ここでは の状況を考える。
には点が含まれないので, には必ず点が選ばれる事になる。 には少なくとも点が 個含まれなければならないという条件が満たされるので, 上の点は のどちらか, 上の点は のどちらか, 上の点は のどちらかを選べば良い。これら 点の選び方は 通りである。
これらのことから,(i)の状況において, 点の選び方は 通りである。
(ii)選んだ点を 個も含まない直線が であるとき
の対称性から,(i)と全く同様の議論をすれば,(i)と場合の数が同じになるはずなので, 通りである。
(iii)選んだ点を 個も含まない直線が であるとき
の選び方は 通りある。ここでは の状況を考える。このとき と には少なくとも点を 個含む。
ここで, に何個ずつ点が含まれるかを考える。 に含まれる点の個数をそれぞれ とすれば, という数の組み合わせが考えられる。
まず について考える。 には点が含まれないので, には必ず点が選ばれる事になる。 には少なくとも点が 個含まれなければならないという条件が満たされるので, 上の点は のどれか, 上の点は のどれかを選べば良い。これら 点の選び方は 通りである。
のときも同様に考えれば,それぞれ 通りである。
次に について考える。 上で という点が含まれ, 上で という点が選ばれたとする(つまりそれぞれの直線上で選ばれた 点の 座標が等しい状況を考える)。このとき, を のうちの とは異なる数として, と 上の両方に点が少なくとも 個あることから, に必ず点が選ばれることになる。 の選び方は 通りであるから,この状況での場合の数は 通り。
それぞれの直線上で選ばれた 点の 座標が等しくはない状況を考える。 上の 点のうち, 座標が揃っている点は 点必ず存在する。その点を と表す。 の選び方は 通りである。 と仮定したとき, 点のうちの残り 点の選び方は もしくは の 通りである。そして,最後の 点については の 通りのうちからどこをとってもよい。よってこの状況での場合の数は 通りである。 よって, のとき 通りである。
のときも同様に考えれば,それぞれ 通りである。
これらのことから,(iii)の状況において, 点の選び方は 通りである。
(i),(ii),(iii)より,求める場合の数は 通りである。
横の場合は縦の場合との対称性で答えが同じになりますが,縦横 本ずつの場合もありますから,骨が折れる問題です。
(2)についても同様に緻密な場合分けが必要になります。
に何個ずつ点が含まれるかを考える。これらは少なくとも 個の点を含むので, 本の直線のうち, 本だけが 個点を含み,そのほかの 本には点が 個のみ含まれる。 個点を含む直線を とする。 の選び方は 通りである。ここでは の状況を考える。 上で 点を選ぶ選び方は 通りである。ここでは が選ばれたとする。
についても,それぞれが少なくとも 個の点を含むので, 本の直線のうち, 本だけが 個点を含み,そのほかの 本には点が 個のみ含まれる。 個点を含む 本の直線を とする。
まず, の場合を考える。 上ではすでに があるから, のどこかに残り 点を選ぶ必要がある。 上ではすでに があるから, 上には点は選ばれない。よって,すでに選ばれている 以外の 点については がそれぞれちょうど 点ずつ点を含むような場合を考えればよく, 通りである。
の場合についても同様に考えれば, 通りである。
次に の場合を考える。 上ではすでに があるから, 上には点は選ばれない。また, 上ではすでに があるから, 上には点は選ばれない。よって, 上にはちょうど 点, 上にはちょうど 点選ばれるように 点を配置すれば良い。 上の 点の選び方は 通りであり,例えば が選ばれたとすると,最後の 点は で決定するので最後の 点の選び方は 通りに必ず定まる。よって, の場合, 通りである。
の場合についても同様に考えれば, 通りである。
よって, が選ばれたという状況のもとでは 通りである。
したがって,求める場合の数は 通りである。
第三問[図形と方程式]
第三問[図形と方程式]
を原点とする座標平面において,放物線 のうち を満たす部分を とする。
(1) 点 が 上を動くとき, を端点とする半直線 が通過する領域を図示せよ。
(2) 実数 に対して,直線 を考える。次の条件を満たす の範囲を求めよ。
上の点 と 上の点 で,3点 が正三角形の3頂点となるものがある。
まず(1)です。この問題は簡単です。半直線の動きを頭の中で想像してみましょう。接点の座標を とすれば, が大きくなるにつれ,半直線は右に傾いていきます。ただ,この半直線が接線となったあと,直線は右ではなく左に傾くようになりますね。イメージとしては以下のような感じです。

とする。これを微分して
であるから, における接線は
この直線が を通るとき,
は にあるから, として における接線は
となる。よって,半直線 の通過する領域は以下の通り。
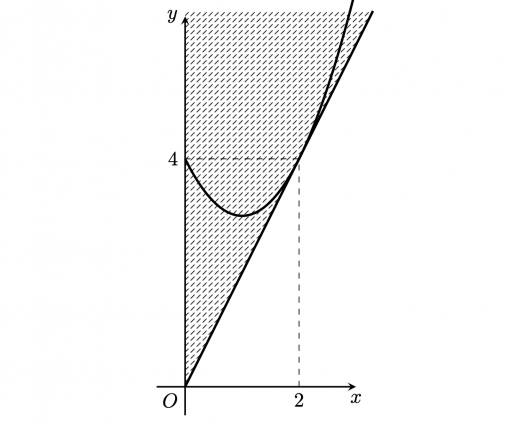
(2)です。(1)で の動く範囲を求めました。半直線 と 軸の正の部分のなす角を とすると, は を動きます。ここで は を満たす数です。
が正三角形をなすには, が必要です。 を固定して を決めたとき, 軸とのなす角が である直線と, 軸とのなす角が である直線上には を取ることができます。よって,これら 本の直線の傾き が, を動かすことによってどう変わるかを見れば良いことがわかります。これを利用して解答をつくりましょう。
半直線 と 軸の正の部分のなす角を とすると,(1)より, は の範囲を動く。ここで は を満たす定数である。 であることを考えると, である。
さて,ある決まった に対し, 軸とのなす角が である直線上, 軸とのなす角が である直線上にはそれぞれ を取ることができる。
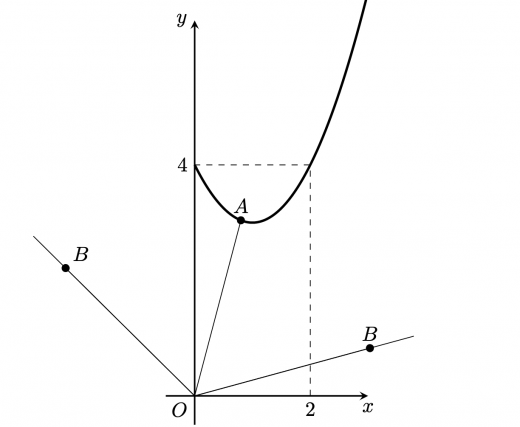
軸とのなす角が である直線の傾きと, 軸とのなす角が である直線の傾きはそれぞれ である。これらが で動く範囲の,その和集合が, の動く範囲である。 を満たす の範囲では は単調増加する。これより ここで より, の範囲は または
ちなみに, の軌跡を直接求めてから の範囲を出すこともできなくはないですが,とてもしんどいです。概略を以下に示します。
とおきます。また,別の表現として とおきます。 を を中心に 回転させることを考えます。つまり, を に回転させることを考えます。加法定理を用いて整理すれば また, も軌跡に含まれる条件です。
ここで, を用いて を消去し, と媒介変数表示で軌跡を求めることができます。概形は以下のようになります。

ちなみに,理系数学の範囲の複素数による回転の話や,回転行列を知っている人ならば, の軌跡を比較的ラクに求めることができます。
また,同様にすると, を を中心に 回転させたときの の軌跡は,
概形は以下のようになります。
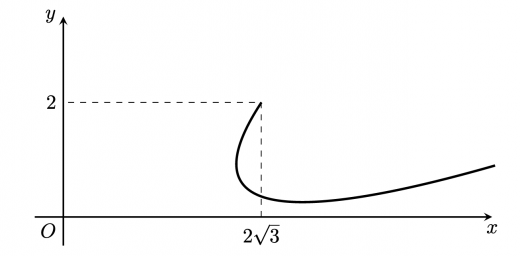
この概形をみると,ここに接線を引いたり,端点を通る直線を引いたりして, の動く範囲を求めれば答えに近づきそうなのはわかっていただけたと思います。 しかし,そんなことをやっているとあっという間に時間はなくなってしまうでしょう。また, が無限に大きくなったときに曲線がどこに漸近して行くかまで考えなければなりません。計算量的にこの解法は実戦では使えないでしょう。
ただ,ここで扱った回転の話はどこかで使えるかもしれないので,覚えておくと良いかもしれません。
第四問[数列]
第四問[数列]
を, を満たす整数とする。 個の整数 から異なる 個を選んでそれらの積をとる。 個の整数の選び方すべてに対しこのように積をとることにより得られる 個の整数の和を とおく。例えば, である。
(1) 以上の整数 に対し, を求めよ。
(2) 以上の整数 に対し, についての整式 を考える。 と を についての整式として表せ。
(3) を で表せ。
理系の第四問と共通の問題です。理系のセットの中でも一番難しいかも?というレベルであり,なんでこれが共通問題なんだろうという疑問を持ちました。
一見してまず感じるのは,問題の設定が複雑そうだ,ということですね。問題の設定さえ理解できれば,(1)は比較的容易に解くことができると思います。
が何を表すかを考えます。 個の整数 の中から,異なる 個を選ぶと, という 個の組み合わせができます。これを全て足すことを考えます。これが になりますね。
さてここで, を考えます。これらを全て展開すると, という数の組み合わせの和が出てきます。ただし,和の中で, において となるものは 度登場します。 となるものは 度だけ登場します。よって, から を引いたものを で割れば, になります。
この議論は約数の総和を求めるときの基本的な公式でも登場します。→約数の総和を求める二つの公式と証明
(2)がかなりの曲者です。とにかく方針が立てづらい問題です。本番の試験では,少し考えて思いつかなければ,違う問題に移るべきでしょう。
が についての整式で表せるということから, の係数 が で表せて,それをつかって を変形すると, の形で表せるかもしれない,と予想しましょう。したがって, をなんとか を使って構成できないか考えてみることから始めます。
とは という 個の整数の中から 個を選んで足したものです。 においては という整数は登場しないため,選び方としては,
- を含めない 個の中から 個を選んだときの総和
- に加え, 個の中から 個を選んだときの総和
の パターンに分類すれば, を使って を表せそうだということに気づきましょう。
ちなみに,これと似たような話として, が同様な考え方をつかって証明できます。ぜひやってみてください。
このことをもとに議論を進めると, という式を得ることができます。この式をよく観察すると, についても解決の糸口が見えてきます。この式が, の漸化式になっていることに気づきましょう。
と合わせれば, の一般的な形を出すことができます。
の 個の整数から 個を選び,その総和を考える。
から 個を選ぶ場合の総和は, に等しい。
を選んだ上で, から残り 個を選ぶ場合の総和は, に等しい。
よって, が成立する。ここで,問題の条件より,この式が成立する の範囲は, である。
について, より,
について, より,
これらを用いると, したがって,
また, により, これと同様に考えれば と表せる。これより,
注意として,漸化式の適用できる範囲を確認するようにしましょう。
最後に(3)です。ここまでできた人にとってはあまり難しくありません。(2)で得た答えを利用します。
(2)において得た答えから, が成立します。 が 両方とも同じ形をした の一次式なので, の の係数には のみが, の の係数には のみが出現します。また, 式ありますから,邪魔な を消せることがわかります。これが使えそうです。
(2)の結果より, が成立する。 の項の係数を比較すると, 一式目の変形 を二式目に代入して, を消去すると,
東大文系数学2020入試過去問解説まとめ
東大文系数学2020入試過去問解説まとめ
全体的に記述しにくい難問が多かったです。本番受験された受験生の方々はとても苦労されたと思います。
第一問は必要条件を見つけて,その十分性を確認するというところまでやって満点になりますが,必要条件を求めるだけでも部分点が来るでしょう。満点の解答をかけなくても,考えた形跡を答案に残しておく癖をつけましょう。
第二問は,場合分けの記述が大変です。具体的な状況を考えても一般性を失わないなら,具体的に考えて議論を進めましょう。
第三問は,この年の問題の中では一番簡単な問題と言えますが,(2)は少し工夫をしないと計算が煩雑になってしまって解けなかった人も多かったかもしれません。
第四問は方針すら見つからなかった人もいたと思います。本番ではいわゆる「捨て問」に当たると思いますが,普段の学習に使うならとても価値のある問題です。よく勉強しておきましょう。
文系数学にしてはかなり難易度高めな問題ばかりでしたね。









