東大文系数学2019入試過去問解答解説
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2019年度入学試験の文系数学について解説します。
第一問[微分]
第一問[微分]
座標平面の原点を とし, を辺の長さが の正方形の頂点とする。3点 はそれぞれ辺 上にあり,3点 および3点 はどちらも面積が の三角形の3頂点であるとする。
(1) と を で表し, それぞれのとりうる値の範囲を求めよ。
(2) の最大値,最小値を求めよ。
この問題は理系の第二問と同じ設定です。文系の問題では小問に分けられ誘導がついています。
(1)です。問題の条件を数式にするところから始めましょう。 の面積が , の面積が という2つの三角形の条件があるので,変数は3つありますが で自由度は に落ちそうです。
よって,最初に の範囲を求め,その後 を動かし,さらにその後で の範囲を求めれば良い,という方針が立てられます。

まず, の面積について, が成立する。また, の面積について, が成立する。これらを同値変形することを考える。 となってしまうと三角形 が潰れてしまうので, が必要。このもと,
の範囲を考える。それには を満たす が存在するような の範囲を求めれば良い。 を消去して整理すれば, とわかる。 より,
また, より,
(2)は(1)がわかれば簡単です。 を で表してみると,三次関数になることがわかります。よって,微分して増減表を描き最大最小を求める,という流れが見えると思います。方針で迷うことはないでしょう。これくらいの計算であれば,ミスなく解き切りたいところです。
より, である。 とおいて, で微分すると, よって, の増減表は以下のようになる。 よって,最大値は また,最小値は のうちの小さい方,つまり となる。
第二問[微積分・ベクトル・図形と方程式]
第二問[微積分・ベクトル・図形と方程式]
を原点とする座標平面において,点 を通り,線分 と垂直な直線を とする。座標平面上を点 が次の2つの条件をみたしながら動く。
条件1:
条件2: 点 と直線 の距離を とし,点 と直線 の距離を とするとき
このとき, が動く領域を とする。さらに, 軸の正の部分と線分 のなす角を とする。
(1) を図示し,その面積を求めよ。
(2) のとりうる値の範囲を求めよ。
座標平面絡みの問題が続きます。問題文が長くてちょっとモヤモヤしますが,言われた通りに条件を数式化していきましょう。
まず条件1について,以下のように同値変形できる。 次に条件2について考える。問題の設定から の傾きは であり,また を通ることから と表せる。また, であり,点と直線の距離の公式より, よって, ここで条件1より, であるから,絶対値がそのまま外せて これらを合わせて,領域 は以下の図の斜線部のようになる。
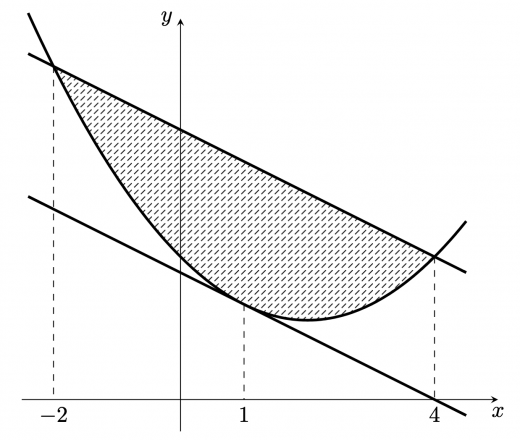
共有点については, を解いて,
また, を解いて, としている。
この図を元に考えれば,求めたい面積は
点と直線の距離の公式(→点と直線の距離公式:例題と5通りの証明)を使うので,絶対値が出てきます。これを場合分けで外さなければならないのか,とちょっと嫌になりますが,条件1を考えるとそのまま外せることがわかって安心しました。
また,積分計算に関しては1/6公式の出番です。時間の大幅短縮につながります。→放物線と直線で囲まれた面積を高速で求める1/6公式
次に(2)です。 は図の斜線部をくまなく動きますから, から放物線に向かって接線を引き,その2本の接線と 軸のなす角が の最大値,最小値になると考えます。ただ,接線を考えてみると,一方の接線の接点は領域 に含まれないことがわかるので注意しましょう。このように図形的に解くのが早くて確実でしょう。
と が重解を持つ条件を考える。これらを連立して, この方程式の判別式を とすれば, であり, となるには, となればよい。
のとき,重解は となるので,接線 は領域 と交点をもつ。よって, がこの接線の領域 における接点 のとき, は最小となる。その値は のとき,重解は となるので,接線 は領域 と交点をもたない。よって, が のとき, は最大となる。その値は が領域 を動く時, はこの間の値を全て取れるので,
の最小値の値はちょっと汚いですね。答えを導いた本番の受験生はとても不安になったことでしょう。
別解として, を の二変数関数とみなして解く方法を紹介します。 を固定して, を動かしたあと, を動かすことを考えます。ちなみに,とても大変で,本番ではできたものではありません。計算力に自信がある人は挑戦してみてはどうでしょうか。商の微分やルートの微分をしなければならないので,範囲としては理系の数学になります。
領域 の図より, であり,この範囲で を固定する。同じく領域 の図から, である。 と表せることから, を固定した状態で を動かすと, ここから, を動かすことを考える。 とおく。これらを で微分して整理すると(ここが大変) の範囲では, より, は単調増加する。よって, の最小値は
また, の増減表を描くと以下のようになる。 よって, の最大値は である。 は の最小値と の最大値の間の値を全て動くので,
第三問[確率]
第三問[確率]
正八角形の頂点を反時計回りに とする。また,投げたとき表裏の出る確率がそれぞれ のコインがある。
点 が最初に点 にある。次の操作を10回繰り返す。
操作:コインを投げ,表が出れば点 を反時計回りに隣接する頂点に移動させ,裏が出れば点 を時計回りに隣接する頂点に移動させる。
例えば,点 が点 にある状態で,投げたコインの表が出れば点 に移動させ,裏が出れば点 に移動させる。
以下の事象を考える。
事象 : 操作を10回行なった後に点 が点 にある。
事象 : 1回目から10回目の操作によって,点 は少なくとも1回,点 に移動する。
(1) 事象 が起こる確率を求めよ。
(2) 事象 と事象 がともに起こる確率を求めよ。
この年の文系のセットでは確率が復活しました!(ただ,理系では今年も確率がありませんでした・・・)
なかなか骨のある確率の問題に見えます。場合分けが多いので本番の緊張した状況では完答は難しかったかもしれません。ただ,もしこの問題で,10回ではなく 回操作を行うとかいてあったらどうでしょうか。数学をよく勉強している人なら,確率漸化式を立てたくなると思います。今回も漸化式を立てて解くことができ,しかもこの解法の方が機械的にできるのでお勧めします。
ただ,確率をどう表すか決める際に少しテクニックが必要です。対称性を用いると変数をより少なくして置くことができます。これをやらないと計算が大変になってしまいます。対称性を利用して変数で確率を表す方法は,東大入試では頻出です。
また,点は操作ごとに必ず隣接する点のどちらかに動きますから,点 は には偶数回操作後, には奇数回操作後しかいないことに注意しましょう。
回操作した後,点 は のどこかにいる。対称性と,全確率が であることから, 回操作した後, にいる確率はそれぞれ以下のようにおける。 次に漸化式を立てることを考える。 回操作した後 にいるのは,
- 2回前に にいて から を通って に来た
- 2回前に にいて から を通って に来た
- 2回前に にいて から を通って に戻って来た
- 2回前に にいて から を通って に戻って来た
の4通りであるから, について という漸化式が立てられる。同様に考えれば, について これより, これを のときの に関する漸化式に当てはめると, また, の に対して, が起こる確率は, のことであるから,
(2)についても確率を変数でおいて考えます。 回操作した後, にいる確率はすでにわかっているので, 回操作した後の確率は漸化式を解かなくても簡単にわかります。
回操作を行うことと,初期位置の から つ分離れていることから, に少なくとも1回到達し,かつ 回目で戻ってこれるのは, に 回目で到達している場合です。このことを利用して答えを求めます。
回操作した後 にいる確率を とおく。 回操作した後, にいるのは,
- もともと にいて から に来た
- もともと にいて から に来た
の2通りであるから, について これより, の に対して, まず,3回の操作後に に到達し,その後の7回の操作で に到達する確率を考える。 から に7回で到達する確率と, から に7回で到達する確率は対称性から同じである。よって,この確率は で求めることができる。同様に考えれば,5回の操作後に に到達し,その後の5回の操作で に到達する確率は, 7回の操作後に に到達し,その後の3回の操作で に到達する確率は, ただこれらには被りがある。
3回の操作後と5回の操作後に に到達し,その後の5回の操作で に到達する確率は, 5回の操作後と7回の操作後に に到達し,その後の3回の操作で に到達する確率は, 3回の操作後と7回の操作後に に到達し,その後の3回の操作で に到達する確率は,初期位置にあった点が,4回で元の位置に戻ってくる確率が に等しいことを利用すると, 3回の操作後と5回の操作後と7回の操作後に に到達し,その後の3回の操作で に到達する確率は, これらにより,被りを差し引くことができ,求めたい確率は で求めることができる。ここで, を代入して計算すれば,答えは
(2)でも対称性が活躍しました。正八角形や円周上など対称性に恵まれた図形の確率は,対称性を活用して計算が簡単にできないか考えましょう。
被りがある部分は共通部分をひくことを考えました。 に 回目で到達している場合の3つの円で構成されるベン図を考えれば状況が掴みやすいです。
第四問[ベクトル・図形と方程式]
第四問[ベクトル・図形と方程式]
を原点とする座標平面を考える。不等式 が表す領域を とする。また,点 が領域 を動くとき, をみたす点 が動く範囲を とする。
(1) をそれぞれ図示せよ。
(2) を実数とし,不等式 が表す領域を とする。また,点 が領域 を動くとき, をみたす点 が動く範囲を とする。 は と一致することを示せ。
まず(1)です。領域 は正方形を表します。もし であったなら話は簡単です。 の一方を固定して,もう一方を動かせばよいのです。例えば で一点を固定してもう一点を動かせば, はその点を中心とする と同じ大きさの正方形上を動きます。よって, を 内で動かせば, よりもう一回り大きい正方形が出現することが,容易に想像できます。イメージとしては,正方形のスタンプを用意し,中心が領域 内から出ないような範囲で,このスタンプをつかってベタ塗りする感じです。
ここで,対称性から, の動く範囲は, と変わらないことがわかります。よって,前段落の議論をそのままそっくり使えます。
領域 について考える。問題の不等式について,
(i) のとき,
(ii) のとき,
(iii) のとき,
(iv) のとき,
よってこれを図示すると以下のようになる。
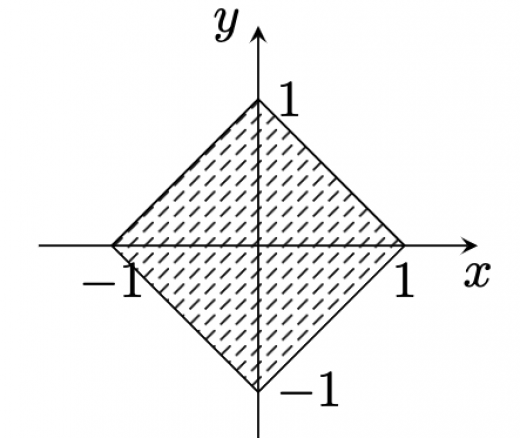
次に領域 について考える。点 は を満たすとする。 が領域 を動く時,対称性から も領域 を動く。よって,点 が領域 を動くとき, をみたす点 が動く範囲は に等しいので,これを考えることにする。
最初に を固定する。ここで を動かせば,点 は を中心とする領域 と合同な領域を動く。次に を動かせば, は を中心とする正方形の通過領域となり,これを図示すると以下のようになる。

次に(2)です。問題の主張が正しいことはなんとなくわかると思いますが,どのように証明するかは少し難しいです。
が,中心が である領域 を動くことと, が,中心が である領域 を動くことは対応することに気づきましょう。
つまり, と置いて, とすると, はどちらも領域 を動くということです。
そして, の基準を点 でとりなおす,つまり として を表し直せば, が引き算で相殺されることがわかります。ほぼ答えを書いてしまいましたが,以下解答例としてまとめます。領域 内の新たな点をとったという意味を強調すべく,名前を点 ではなく点 としています。
と置いて,領域 内を動く点 に対し, とすると,点 は領域 内全体を動く点である。
このとき, よって,点 が動く領域 は領域 と一致する。
また,別解として同値変形を利用することが考えられます。文字は増えてしまいますが,こちらの方が機械的にできるので,同値変形の処理が得意な人にとってはラクかもしれません。
まず,領域 について考える。 とおく。 は領域 を動くので, また, これより, を満たす が存在するような の条件を求めれば良い。 を使って を消去すれば, を満たす が存在するような の条件を求めれば,領域 がわかる。
次に領域 について考える。 とおく。 は領域 を動くので, また, これより, を満たす が存在するような の条件を求めれば良い。 を使って を消去すれば, を満たす が存在するような の条件を求めれば良い。 と置けば, を満たす が存在するような の条件を求めれば,領域 がわかることになり,これは領域 の条件と完全に一致する。
東大文系数学2019入試過去問解説まとめ
東大文系数学2019入試過去問解説まとめ
座標平面上で図形を考えさせる問題が多かったですね。東大受験生にとってこの分野は要注意です。よく勉強しておきましょう。
第一問,第二問については,誘導が丁寧でしたし,ぜひ解ききりたいところです。
第三問の確率の問題についてですが,(1)は簡単です。(2)が場合分けでやろうとするととても大変だったでしょう。場合分けが面倒そうだと思った時は,今回紹介した解答例のように, 回の操作をした後の状況を考えてみると,漸化式を解くことで対処できることがあります。
第四問は答え方の幅はとても広そうです。感覚的には当たり前なことをきちんと説明する解答を作らなければならないからです。どこまで厳密に記述するか迷いどころですが,この記事の解答例を一つの参考にしていただければと思います。
第二問の別解の微分計算をやった人は,根性がありますね。









