相似変換
更新
相似変換 に関する3記事をまとめました。くわしくは各リンク先を見てください。
全ての放物線は互いに相似である。
任意の円は相似である。
特に,接する2つの円の相似の中心は接点である。
ケージーの定理(Casey's Theorem)
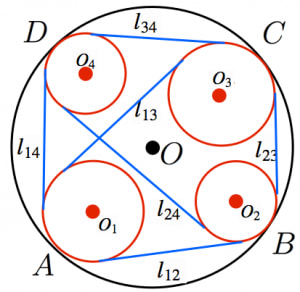
互いに交わらない4つの円 がそれぞれ点 で別の円 に(この順番に)内接しているとき,円 と の共通外接線の長さを とおくと,
更新
相似変換 に関する3記事をまとめました。くわしくは各リンク先を見てください。
全ての放物線は互いに相似である。
任意の円は相似である。
特に,接する2つの円の相似の中心は接点である。

互いに交わらない4つの円 がそれぞれ点 で別の円 に(この順番に)内接しているとき,円 と の共通外接線の長さを とおくと,
人気記事