座標,ベクトル に関する51記事をまとめました。くわしくは各リンク先を見てください。
点と直線の距離公式
点 (x0,y0)と直線 ax+by+c=0 の距離は,
a2+b2∣ax0+by0+c∣
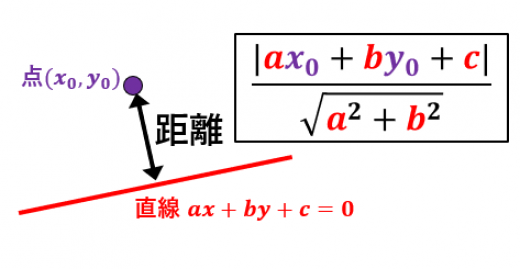
→点と直線の距離公式:例題と5通りの証明
公式
座標平面上の異なる二点
(x1,y1),(x2,y2) を通る直線の方程式は次の三種類ある。
-
y−y1=x2−x1y2−y1(x−x1)
-
(x2−x1)(y−y1)=(y2−y1)(x−x1)
-
(xy)=(x1y1)+t(x2−x1y2−y1)
→二点を通る直線の方程式の3タイプ
極座標とは,原点からの距離
r
と「角度」
θ
という2つの数字を使って平面上の点の位置を表すような方法です。
→直交座標と極座標(2次元)の変換とメリットの比較
垂直条件1
二直線:y=m1x+n1 と y=m2x+n2 が直交する ⟺m1m2=−1
→垂直な直線の方程式の求め方と応用【垂直条件】
単位ベクトルの定義
単位ベクトルとは,長さ(大きさ)が1のベクトルのことです。
→単位ベクトルの求め方といろいろな具体例
ベクトルとは,
-
(主に高校数学で)向きと大きさを持った量,実数二つ組または三つ組
-
(主に大学数学で)ベクトル空間の元
-
(主に日常会話で)方向性
→ベクトルという言葉の意味
公式
A(xA,yA),B(xB,yB)
のとき
-
線分
AB
を
m:n
に内分する点
P
の座標は
(m+nnxA+mxB,m+nnyA+myB)
-
線分
AB
を
m:n
に外分する点
Q
の座標は
(m−n−nxA+mxB,m−n−nyA+myB)
→内分点,外分点の公式と証明
原点と点Aとの距離
d=(ax)2+(ay)2
d=(ax)2+(ay)2+(az)2
→平面,空間上の2点間の距離について
OA=ba=⎝⎛a1a2a3⎠⎞, OB=b=⎝⎛b1b2b3⎠⎞
としたとき,三角形 OAB の面積 S は以下のように表せる。
-
S=21∥ba∥2∥b∥2−(ba⋅b)2
-
S=21(a2b3−a3b2)2+(a3b1−b3a1)2+(a1b2−a2b1)2
→三角形の面積のベクトル・成分を用いた公式
例題
座標平面上に2点 A(−1,1),B(3,3) がある。
線分 AB の長さを求めよ。
→線分の長さの求め方(2点間・放物線・二等辺三角形・弦)
一般のベクトルを位置ベクトルで表す公式
原点を O として,2点 A(a),B(b) を結ぶベクトル AB を位置ベクトルを用いて表すと,
AB=OB−OA=b−a
→位置ベクトルの定義と基本例題の解説
内積の定義
2つのベクトル a,b に対して,∣a∣∣b∣cosθ のことを内積と呼び,a⋅b と書く。
→ベクトルの内積の性質と公式
サラスの公式
3×3の行列の行列式は
「左上から右下にかけて足す」マイナス「右上から左下にかけて足す」
という方法で計算できる。
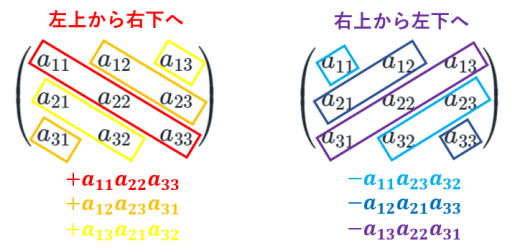
→サラスの公式と使い方
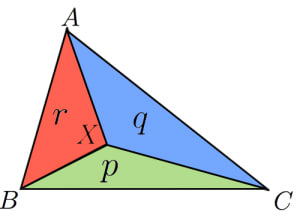
三角形
ABC
内に点
X
があり,pXA+qXB+rXC=0
が成立するとき,面積比は
△XAB:△XBC:△XCA=r:p:q
→ベクトルの定番問題を一瞬で解く公式
xy 座標平面における直線の方程式には,いくつかの表し方がある。
- y=mx+n(傾きと切片による表現)
- ax+by+c=0(一般形)
→直線の方程式の一般形が嬉しい3つの理由
2点
(a,0),(0,b)
を通る直線の方程式は,
ax+by=1
3点
(a,0,0),(0,b,0),(0,0,c)
を通る平面の方程式は,
ax+by+cz=1
→切片方程式とその証明に関すること
束の考え方
s
と
t
は実数で少なくとも一つは
0
でないとする。
sf(x,y)+tg(x,y)=0 が表す図形は,
f(x,y)=0 が表す図形と g(x,y)=0 が表す図形の交点(が存在すれば)を全て通る。
→束の考え方と例題(直線,円,一般論)
三次元空間における直線の基本形:
点 A(a) を通り,方向ベクトルが d であるような直線の方程式は,媒介変数 t を用いて p=a+td と表される。
→三次元空間における直線の方程式
二直線のなす角の求め方は「tanによる方法」「cosによる方法」の2通りある。

→二直線のなす角を求める2通りの方法と比較
公式1
中心が
(a,b,c) で半径が
r
の球面の方程式は,
(x−a)2+(y−b)2+(z−c)2=r2

→球面の方程式に関する5つの公式と具体例
ベクトルの内積を用いて余弦定理を証明できるが,循環論法にならないように気をつける必要がある。
→ベクトルの内積を用いた余弦定理の証明
円の接線の方程式
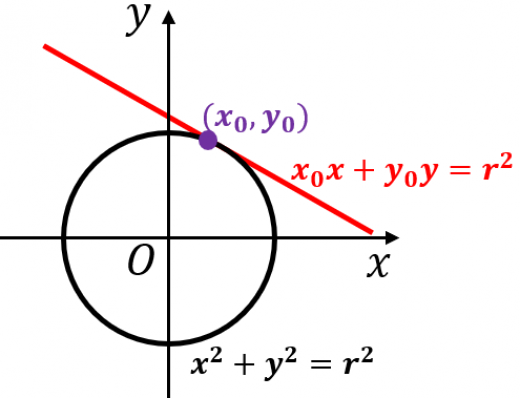
座標平面において,円:
x2+y2=r2
上の点
(x0,y0)
における接線の方程式は,
x0x+y0y=r2
→円の接線の方程式を求める公式の3通りの証明
受験生なら一度はやっておきたい軌跡の有名問題を解説します。実は,反転という幾何学の手法を背景とする問題です。
→反転にまつわる軌跡の有名問題
四点が同一平面上にある条件1(ベクトル)
三次元空間内の四点
A,B,C,D
が同一平面上にある
⟺
三点
A,B,C
が同一直線上にある,または
AD=pAB+qAC
を満たす実数
p,q
が存在する。
→四点が同一平面上にあるための二つの条件
2つの平面
a1x+b1y+c1z+d1=0,a2x+b2y+c2z+d2=0
のなす角を
θ
とすると,
cosθ=a12+b12+c12a22+b22+c22∣a1a2+b1b2+c1c2∣
→2平面のなす角の定義と求め方
ベクトル方程式の公式をまとめました。全て丸暗記する必要はありませんが,◯◯のベクトル方程式は?と聞かれたときにすぐに立式できるようになっておきましょう。
→ベクトル方程式の公式一覧
問題
a,b は正の実数とする。xy 平面上に曲線 C1:y=(x−a)2,C2:y=b−x2 がある。点 P を (a,0) とする。
以下の問いに答えよ。
(1) C1 と C2 が異なる2つの交点を持つ条件を a,b の不等式により表せ。
(2) 以下 a,b は(1)で求めた条件を満たすものとする。P1,P2 を C1 と C2 の交点とする。ただし P1 を x 座標の小さいほうとする。今,b を固定したとき ∠P1PP2=90∘ となるような a が存在する。b の値の範囲を求めよ。
(3) 今,∠P1PP2=90∘ を満たしているとする。P,P1,P2 を通る円を C とする。C と y 軸の交点の座標を b を用いて求めよ。
(4) 円 C の中心を Q とおく。△OP2Q が正三角形であるとする。このとき b の値を求めよ。
→図形と方程式・ベクトル分野:練習問題一覧|入試数学コンテスト過去問集
問題(大阪大学2024)
空間内の2直線 l,m はねじれの位置にあるとする。l と m に直交する直線がただ1つ存在することを示せ。
→ねじれの位置にある2直線に関する問題~大阪大学2024
内積の定義1
ベクトル a と b に対して,∣a∣∣b∣cosθ を内積と言う。ただし,θ は a と b がなす角。
→ベクトルの内積と外積の意味と嬉しさ
xy
座標平面における直線は
ax+by+c=0
という形で表せる。
同様に,xyz
座標空間上の平面の方程式は
ax+by+cz+d=0
という形で表せる。
→平面の方程式とその3通りの求め方
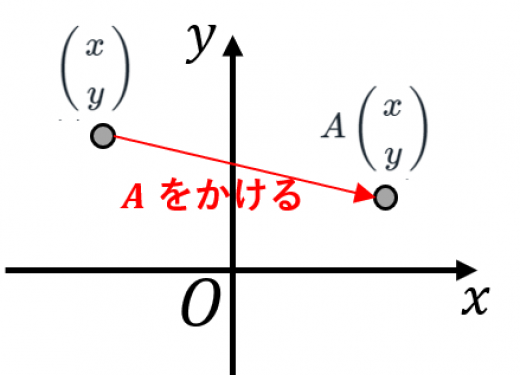
一次変換とは
一次変換とは,行列
A
のかけ算による変換です。行列
A=(acbd)
に対応する一次変換は,(xy)
を
A(xy)=(ax+bycx+dy)
に写します。
→一次変換の意味と重要な5つの例(折り返し・回転・対称移動)
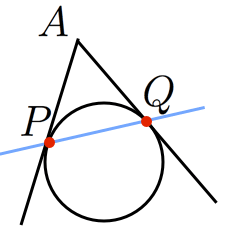
極線の方程式(原点中心の場合)
円 x2+y2=r2 に対して,外側の点
A(x1,y1)
から引いた2本の接線の接点を
P,Q
とおく。
- 直線 PQ を(極 A に対する)極線と呼ぶ。
- 極線の方程式は x1x+y1y=r2
→極線の方程式の証明と応用
三角形 ABC とその内部の点 P について
AX2+BX2+CX2
が最小になるのは,P が三角形 ABC の重心であるときである。
つまり,三角形 ABC の重心を G とすると
AX2+BX2+CX2≧AG2+BG2+CG2
が成り立ち,X=G のとき等号が成立する。
→三角形における距離の二乗の和の公式
2直線 y=m1x+n1,y=m2x+n2 が直交するのは m1m2=−1 となるときである。
→法線ベクトルの3通りの求め方と応用
点と平面の距離公式
xyz 座標平面上で ax+by+cz+d=0 という式は平面を表す。この平面と点 (x0,y0,z0) の距離は,a2+b2+c2∣ax0+by0+cz0+d∣

→点と平面の距離公式と例題・2通りの証明
正射影ベクトルの公式
ベクトル
b
を
a
が定める直線に正射影したベクトルは,∣a∣2a⋅ba
→正射影ベクトルの公式の証明と使い方
放物線をその軸に関して回転させたときにできる図形を回転放物面と言う。
xyz
座標空間において,放物線
z=ax2+b
を
z
軸のまわりに回転させたときにできる図形の方程式は
z=a(x2+y2)+b
である。
→回転放物面の方程式と東大の問題
マンハッタン距離
座標平面上の2点
A(a1,a2),B(b1,b2)
の間の距離を
d(A,B)=∣a1−b1∣+∣a2−b2∣
で測ったものを
L1
距離(マンハッタン距離)と言う。
→L1距離(マンハッタン距離)の意味と性質
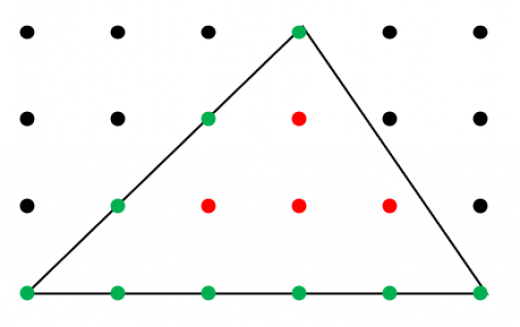
ピックの定理(Pick's theorem)
頂点がすべて格子点上にある多角形の面積は
内側の格子点数+辺上の格子点数÷2−1
→ピックの定理
オイラー線

任意の三角形において,外心を
O,重心を
G,垂心を
H
とおくとき,
O,G,H は一直線上にあり,OG:GH=1:2
→オイラー線の3通りの証明
正二十面体のいろいろな量
1辺の長さが1の正二十面体について,
- 表面積は 53
- 最長の対角線の長さ(直径)は 25+5,外接球の半径は 410+25
- 体積は 1215+55
- 内接球の半径は 1233+15
→正二十面体の対角線・体積・内接球などを座標で計算
重心座標の定義
点 X
が
x=p+q+rpa+qb+rc
を満たすとき,X
の重心座標を,[p,q,r] とする。
→三角形の重心座標とその応用
フォイエルバッハの定理(Feuerbach)
任意の三角形において
- 内接円と九点円は内接する。
- 傍接円と九点円は外接する。
→フォイエルバッハの定理と計算による証明
ロドリゲスの回転公式(ベクトル)
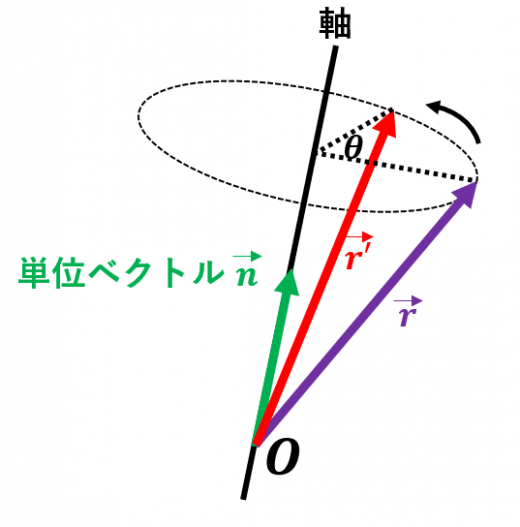 三次元空間において,n を軸として,r を θ 回転させた点 r′ は,
三次元空間において,n を軸として,r を θ 回転させた点 r′ は,
r′=(cosθ)r+(1−cosθ)(r⋅n)n+(sinθ)(n×r)
→ロドリゲスの回転公式(3次元の回転行列)
定義(ヘルマート変換)
XY=ax−by+c=bx+ay+d
という式で (x,y) を (X,Y) にうつすような変換をヘルマート変換と言う。
→ヘルマート変換の意味・アフィン変換との関係
四元数を考える理由
-
数学的に美しい
-
三次元空間中での回転を簡単に記述できる
→四元数と三次元空間における回転
スカラー三重積の定義
3つの空間ベクトル
a,b,c
に対して
a⋅(b×c)
をスカラー三重積と言う。
→スカラー三重積とベクトル三重積
公式1
曲面
f(x,y,z)=0
の
(x0,y0,z0)
における接平面の方程式は,
A(x−x0)+B(y−y0)+C(z−z0)=0
ただし,A=fx(x0,y0,z0),B=fy(x0,y0,z0),C=fz(x0,y0,z0)
→接平面の方程式の求め方
足し算とスカラー倍ができるような代数系をベクトル空間(線型空間)という。
→ベクトル空間と次元
ガウスの発散定理の大雑把なイメージ
閉曲面 S を貫く水の総量は,その内部 V から湧き出したり,吸い込まれたりする量に等しい。
→ガウスの発散定理・ストークスの定理の証明
グリーンの定理
(単純)閉曲線 C と,C で囲まれた領域 D を考える。D 上で C1 級の任意の関数 P(x,y),Q(x,y) に対して以下が成り立つ。
∮C(P(x,y)dx+Q(x,y)dy)=∬D(∂x∂Q−∂y∂P)dxdy
→グリーンの定理











 三次元空間において, を軸として, を 回転させた点 は,
三次元空間において, を軸として, を 回転させた点 は,




