直交座標と極座標(2次元)の変換とメリットの比較
極座標とは,原点からの距離 と「角度」 という2つの数字を使って平面上の点の位置を表すような方法です。
この記事では, 極座標の意味 , 直交座標と極座標の変換方法 などを解説します。
極座標とは
極座標とは
平面上の点の位置は,二つの数字を使うことで表現できます。例えば, 直交座標( 直交座標,デカルト座標)では で点の位置を表します。
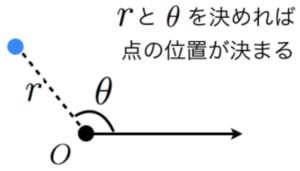
一方, 極座標では で点の位置を表します。ただし
-
は原点からの距離を表し,動径と呼ばれます。
-
は始線(原点を通る基準の半直線, 軸の正の向きと一致させるのが慣例)から反時計周りに測った角度を表し,偏角と呼ばれます。

図において,点 の位置は
直交座標で と表してもよいし,
極座標で
と表してもよい。
直交座標と極座標の変換(2次元)
直交座標と極座標の変換(2次元)
 同じ点
が直交座標で
,極座標で
と表されているとき,
同じ点
が直交座標で
,極座標で
と表されているとき,
が成立します。これにより,極座標,直交座標のいずれかが分かればもう一方もすぐに分かります。
・極座標→直交座標
を計算するのみです。
極座標で
であるような点を直交座標で表すと,
より,
・直交座標→極座標
という2つの式を変形すると, となります。この1つめの式から が計算でき,2つめと3つめの式から が計算できます。
ただし,上の3式を満たす は無数にあるので, と制限することが多いです。
であるような点を極座標で表す。
まず,
次に, と から となる。
直交座標と極座標のメリットの比較
直交座標と極座標のメリットの比較
直交座標のメリット
- どの座標軸も対等であり,多くの場合微分や積分の計算が楽。
- 一つの点と二つの実数の組 の間に1対1対応がある。
注:極座標では一つの点を表す が無数にあります。原点の扱いも不便です。
極座標のメリット
- 「距離」と「角度」という物理的な量を用いて表現するので,イメージしやすい。物理現象の記述に便利なことが多い(例えばクーロン力や重力の記述など)。
- 極座標で表す方が簡潔な図形の方程式もけっこうある。
例えば,円の方程式は よりも の方が簡潔。他にもカージオイドやレムニスケートなど。→媒介変数表示された有名な曲線7つ
例えば と で点の位置を表現することもできますが,利点はなさそうです。











