空間図形 に関する23記事をまとめました。くわしくは各リンク先を見てください。
(i)1辺の長さが
a
の正三角形の面積
S
は,
S=43a2
(ii)1辺の長さが
a
の正四面体の体積
V
は,V=122a3
→正三角形の面積,正四面体の体積を求める公式
正多面体は5種類しかない
正多面体は,正4面体,正6面体,正8面体,正12面体,正20面体の5つのみ。
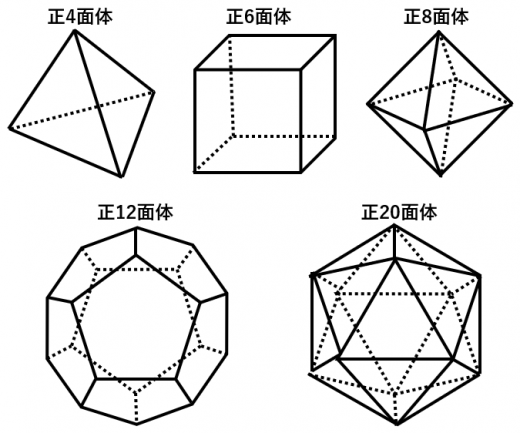
→正多面体が5種類しかないことの2通りの証明
球の体積と表面積の公式
半径
r
の球の表面積は
S=4πr2,
球の体積は
V=34πr3
である。
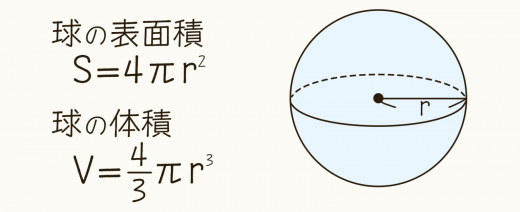
→球の体積と表面積の公式の覚え方・積分での求め方
原点と点Aとの距離
d=(ax)2+(ay)2
d=(ax)2+(ay)2+(az)2
→平面,空間上の2点間の距離について
体積を計算するための公式を整理しました。立方体からはじめて難しい公式まで一覧にしましたが,特に重要なのは,
- 柱体の体積:底面積×高さ
- 錐体の体積:底面積×高さ÷3
の2種類です。
→体積を求める公式一覧
立体の表面積を計算するための公式を整理しました。立方体からはじめて難しい公式まで一覧にしましたが,重要なのは,
- 「表面積は,すべての面の面積を求めて足し上げる」
- 球の表面積公式だけは覚えるべし
という2点です。
→表面積を求める公式一覧
三角錐,四角錐,円錐などの錐体の体積は
31×底面積×高さ
→錐体の体積に1/3がつくことの2通りの説明
問題(大阪大学2024)
空間内の2直線 l,m はねじれの位置にあるとする。l と m に直交する直線がただ1つ存在することを示せ。
→ねじれの位置にある2直線に関する問題~大阪大学2024
内接球の半径を求める公式
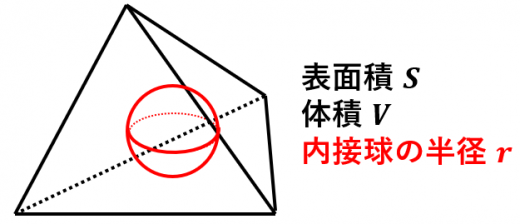
多面体において表面積を
S,体積を
V,内接球の半径を
r とおくと,
V=31rS
→内接球の半径を求める公式と例題・証明
等面四面体
全ての面が合同な四面体の問題は直方体への埋め込みを考えればほぼ確実に解ける。
→等面四面体とその性質
正八面体を上から見た図と,1つの面と平行な平面で切った切断面の形は覚えておくとよい。
→正八面体を上から見た図と東大の問題
四平方の定理(四面体)
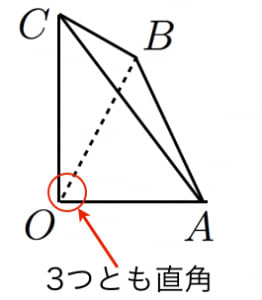
4つの面のうち3つが直角三角形である図のような三角錐(直角三角錐,三直角四面体)において,
∣ABC∣2=∣OAB∣2+∣OBC∣2+∣OCA∣2
→四平方の定理(図形の面積と正射影)
四面体の重心
四面体において,頂点と対面の重心を結ぶ四本の線分は一点で交わる。これを四面体の重心という。
→四面体の重心の存在証明と応用例
正四面体
ABCD
の中心を
G
とする。このとき,正四面体の中心角
θ=∠AGB
は,
cosθ=−31
を満たす。
具体的には,θ≒109.5∘
→正四面体の中心角の2通りの求め方
→正六面体と正八面体の双対関係と京大の問題
楕円体・回転楕円体
-
a2x2+b2y2+c2z2=1
で表される曲面を楕円面と言う。
-
楕円面を表面とする立体
a2x2+b2y2+c2z2≤1
を楕円体と言う。

-
特に,a,b,c のうち2つ以上が等しい場合,楕円面のことを回転楕円面と言い,楕円体のことを回転楕円体と言う。
-
a=b=c の場合は球面・球になる。
→楕円体・回転楕円体の意味と体積・表面積
直辺四面体
四面体 ABCD において,以下は同値:
-
AB⊥CD,AC⊥BD
-
AB⊥CD,AC⊥BD,AD⊥BC
-
四面体 ABCD に垂心が存在する(頂点から対面におろした4本の垂線が1点で交わる)。
-
AB2+CD2=AC2+BD2=AD2+BC2
-
対辺の中点同士を結ぶ3本の線分の長さが等しい
→直辺四面体(垂心四面体)と24点球の定理
1辺の長さが1の正12面体について,
-
異なる2頂点間の長さは5種類あり,それぞれ 1,21+5,22+10,23+5,23+15
特に最長の対角線の長さは 23+15
-
外接球の半径は 43+15
-
内接球の半径は 4025+115
-
表面積は 325+105
-
体積は 415+75
→正12面体のいろいろな計算(対角線・表面積・体積・内接球・外接球)
球面上の三角形の面積
半径
R
の球面上にあり,内角の大きさが
A,B,C
である三角形の面積は,
S=R2(A+B+C−π)
→球面上の三角形の面積と内角の和
半径が
R
の球面上の
n
角形について,その面積を
S
,内角を
θ1,θ2,⋯,θn
とおくと,
S=R2{i=1∑nθi−(n−2)π}
→球面上の多角形の面積と美しい応用
平行六面体
各面が平行四辺形である六面体のことを平行六面体と呼ぶ。

→平行六面体の話題(体積・分類・角度の三角不等式)
→半正多面体と準正多面体
カラテオドリの定理
A
が
Rn
の部分集合
S
の凸包に含まれているとき,S
から
n+1
個の点をうまく選んでくれば,その
n+1
個の点の凸包に
A
が含まれるようにできる。
→凸包に関するカラテオドリの定理とその証明











