正六面体と正八面体の双対関係と京大の問題
正六面体と正八面体は互いに双対である。
立体の双対とは
立体の双対とは
立体 が与えられたときに,以下のように立体 を構成できます。
-
の各面の中心(重心)を の頂点とする。
-
の隣り合う つの面に対応する の つの頂点を辺で結ぶ。
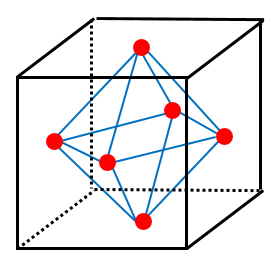
例として,正六面体(立方体)の双対 を考えてみます。 の頂点は正六面体の各面の重心( つの赤い頂点)になります。そして,それらについて「もとの正六面体で隣り合う面に対応する点のペア」を辺で結びます。つまり,正六面体の辺 本に対応して, でも辺が 本引かれることになります。
このようにしてできる立体 は正八面体となることが分かります。逆に,正八面体の双対を取ると正六面体になります。
同様に,正12面体と正20面体は互いに双対の関係にあります。
京大の問題
京大の問題
2001年京大理系第4問です。いろいろな考え方がありますが,正六面体と正八面体の双対性を知っていたらほんの少しだけ有利です。
空間内の正八面体の頂点 とベクトル に対し, のとき が成り立っているとする。このとき, と異なる全ての に対して
となるような が存在することを示せ。
考え方と解答
考え方と解答

図のように座標を設定できます。 が「右」を向いているときは, として緑の頂点を選べば は左の方を向いているので内積が負になりそうです。
が他の方向(左,上,下,奥,手前)を向いているときも同様に考えることができそうです。
まず, の中に等しいものがある場合, という条件が成立しない。よって は全て異なる。
が(6個の向きの中で)右を向いているとき,つまり ,,,,, の中で が一番大きい場合を考える。このとき, とすれば, に対して であることが確認できる。
(実際, は ,, のどれか)
対称性より,他の場合も適切な を取ってこれる。
今回紹介した方法,考え方はとても自然だと思いますが,きちんと解答にするのはけっこう大変です。











