集合,命題,論証
更新
集合,命題,論証 に関する25記事をまとめました。くわしくは各リンク先を見てください。
任意の集合 に対して以下が成立します。
これをド・モルガンの法則と言います。
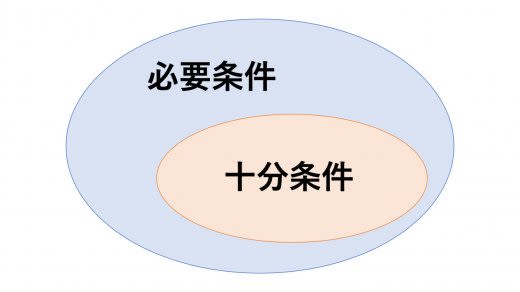
必要条件・十分条件・必要十分条件 について,基礎からわかりやすく解説します。
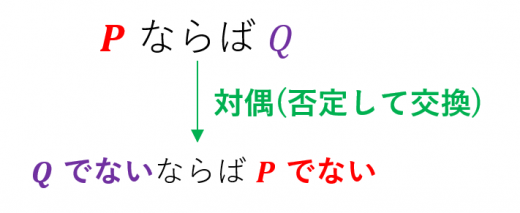
「 ならば 」に対して,「 でないならば でない」のことを対偶と言います。
- 開区間とは,「 より大きく より小さい数全体の集合」のこと
- 閉区間とは,「 以上 以下の数全体の集合」のこと

集合の記号とその意味について整理しました。高校数学で習う(大学入試で必要な)ものと習わないものそれぞれ紹介します。
集合 の補集合とは,「全体」の中で に含まれない要素をすべて集めたもの。
有理数とは, の形で表せる数のこと。
背理法とは,
①命題が正しくないと仮定する
②その結果,矛盾してしまう
③よって,命題は正しい
という流れで証明を行う手法のこと。

座標平面における領域 で定まる図形 を考える。 に対して,原点を中心とする回転や平行移動を,何回か行って得られる図形を 個用意し,それぞれ とする。
このとき, により座標平面を覆うことのできる の最小値を求めよ。
個のものを グループに分けると,必ず 個以上属するグループが存在する。

より一般に, 個のものを 個のグループにわける。 が より大きいなら,必ず2つ以上のものが属するグループが存在する。
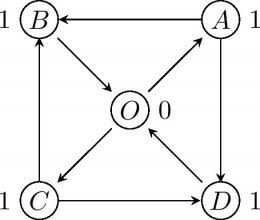
JMO 星団は,はじめ 5 つの星 ,,,, からなっており,それぞれの星には重要度とよばれる値が割り当てられている。 の重要度は 0 であり,,,, の重要度は 1 である。また, から および へ, から および へ, から ヘ, から および へ, から へ向かう一方向の直行便が開設されており,ほかに直行便はない。
JMO 星団では星の老朽化を防ぐために,次の一連の行動からなる操作を定期的に行うことにした。
(1) 今あるすべての直行便を廃止し,すべての星を破壊する。
(2) 今回の操作の (1) で廃止したすべての直行便 に対して,それに対応する星 を 1 つずつ建設する。その後, の重要度として, が出発する星と到着する星の重要度の和を割り当てる。
(3) 今回の操作の (1) で廃止した 2 つの直行便の組 であって, が到着する星と が出発する星が一致するようなものすべてについて, から に向かう一方向の直行便を開設する。
このとき,100 回目の操作で建設した星の重要度の総和を求めよ。
全ての人はハゲである
「自分自身を含む集合」について考えてみます。ラッセルのパラドックスという有名な話題です。
全体で見たときの相関と分割して見たときの相関が逆になってしまうことがある。

平面内の部分集合 で,以下の条件を満たすようなものが存在する。
条件「 の分割 が存在して, を平行移動すると と一致し, を回転すると と一致する」
区間 から「線分を三等分して真ん中を取り除く」という操作を無限回繰り返して得られる集合をカントール集合という。

円周率 は無理数である。
有限集合の大きさは要素数ではかれる。
無限集合の大きさの表現には濃度を用いる。
任意の と に対して
が成立するとき,集合関数 は劣モジュラ関数であると言う。
「任意の」とは「全ての」という意味です。 という記号を使って表すことがあります。
任意の集合 に対して,
数学の様々な場面で登場する重要な概念「同値関係」について解説します。同値関係とは,大雑把には「仲間であるという関係」です。
集合 について, から への単射があり, から への単射があれば から への全単射(一対一対応)がある。
を群, をその部分群とする。 に対して を の左剰余類という。
2つの集合 , に対して「 と から1つずつとってきたペアをすべて集めた集合」のことを と の直積集合といい, と表す。つまり,






