シンプソンのパラドックス
全体で見たときの相関と分割して見たときの相関が逆になってしまうことがある。

シンプソンのパラドックスについて,具体例を使ってわかりやすく説明します。
シンプソンのパラドックスの具体例
シンプソンのパラドックスの具体例
シンプソンのパラドックスを理解するためには具体例が一番です。
数学のテストの点数を高校Aと高校Bで比較する。

- 高校Aは理系90人(平均80点),文系10人(平均60点)
- 高校Bは理系10人(平均90点),文系90人(平均70点)
どちらの学校が数学に強いと言えるか?
-
理系,文系別々に考えると高校Bの方が数学に強い。
- 理系の平均点は高校Bの方が高い
- 文系の平均点も高校Bの方が高い
-
全体平均で考えると高校Aの方が数学に強い。
- 高校Aの全体平均は, 点
- 高校Bの全体平均は,
点

考え方によって二つの相反する結論が得られました。これがシンプソンのパラドックスです。
メカニズム
メカニズム
シンプソンのパラドックスのメカニズムを図示しました。
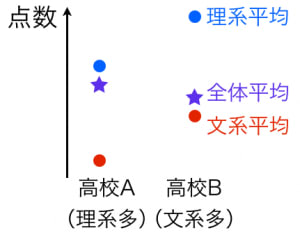
理系,文系それぞれの平均では高校Bが勝っていますが,加重平均を取るときの重みが違うので全体平均では逆転します。
パラドックスの回避
パラドックスの回避
このパラドックスを回避するためにはそれぞれの立場の根拠を明確にすることです。
この例の場合,例えば以下のように説明できます。
- そもそも文系よりも理系の方が数学ができる(専攻と数学の点数には相関がある)
- 高校Aは高校Bに比べて圧倒的に理系が多い
よって,高校Aの全体平均が高いのは当然。全体平均を比べることにあまり意味はない。
高校の教育力を比較するには同じ条件で考えないといけない。そこで,「理系」or「文系」に限定して同じ土俵で考えると高校Bの方が優れていると言える。
「理系」であったとしても「文系」であったとしても高校Bに行った方が数学ができるようになる可能性が高いと言える!
少々強引ですが,以下のような説明も考えられます。
「理系の生徒を多く集めることができた」というのも数学に力を入れている高校の実力のうちだ。だから全体平均で考えるのがよい。
都合の悪い方の説明には一切触れずに,都合のいい方の説明を使うことができるので,高校Aの人は説明2を使い,高校Bの人は説明1を使うでしょう。
どちらの考え方も(根拠とともに)きちんと理解した上で,自分がどちらに賛同するのか決めることが重要です。
私はこの例の場合,説明1に賛同します。
Tag:難しめの数学雑学・ネタまとめ











