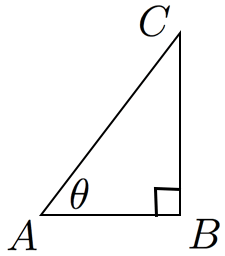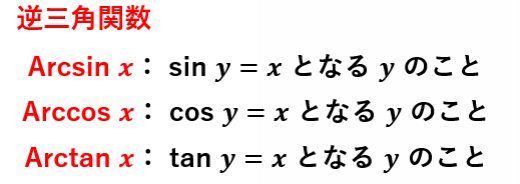三角比・三角関数 に関する44記事をまとめました。くわしくは各リンク先を見てください。
15∘ の三角比は
sin15∘cos15∘tan15∘=46−2=46+2=6+26−2=2−3
である。
→sin15°、cos15°、tan15°【覚えておくと便利な三角比】
正弦定理(簡単バージョン)
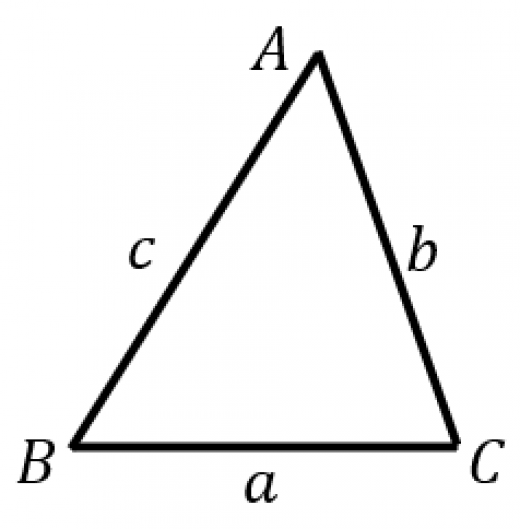
正弦定理とは,三角形において,
sinAa=sinBb=sinCc
が成立するという定理。ただし,
- A,B,C は3つの内角の大きさ。
- a=BC,b=CA,c=AB は3辺の長さ。
→正弦定理の意味と6通りの証明・頻出の応用例
三角関数の定義
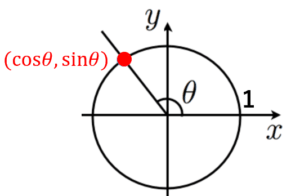
三角関数とは,以下で定義される
sinθ,cosθ,tanθ
のことです。
-
sinθ とは,単位円上の角度 θ に対応する点の y 座標
-
cosθ とは,単位円上の角度 θ に対応する点の x 座標
-
tanθ とは,cosθsinθ のこと
→三角関数の基本公式一覧
secx=cosx1
cscx=sinx1
cotx=tanx1
→三角関数sec, cosec, cotと記号の意味
三角関数の合成公式
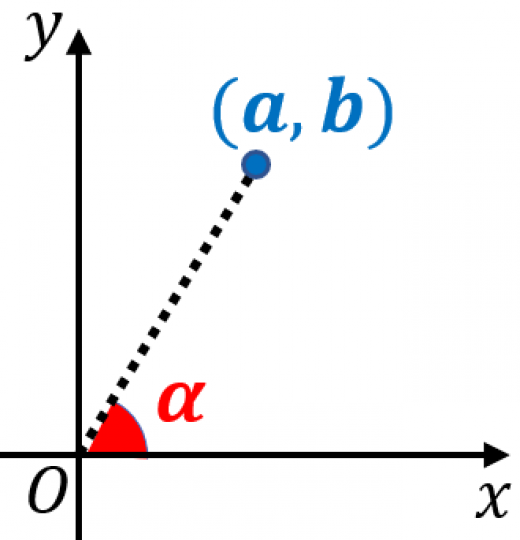
asinθ+bcosθ=a2+b2sin(θ+α)
ただし,α は図のように (a,b) に対応する角度。つまり「x 軸の正の部分を反時計回りにいくら回転したら (a,b) を通るか」を表す角度。つまり,cosα=a2+b2a,sinα=a2+b2b
を満たす。
→三角関数の合成のやり方・証明・応用
三角関数の加法定理
任意の実数 α,β に対して
-
sin(α+β)=sinαcosβ+cosαsinβ
-
sin(α−β)=sinαcosβ−cosαsinβ
-
cos(α+β)=cosαcosβ−sinαsinβ
-
cos(α−β)=cosαcosβ+sinαsinβ
-
tan(α+β)=1−tanαtanβtanα+tanβ
-
tan(α−β)=1+tanαtanβtanα−tanβ
ただし,5,6は tanα,tanβ,tan(α±β) が定義できる場合における式。
→加法定理の証明(一般角に対する厳密な方法)
sinx
および
cosx
は微分すると位相が90度進む。積分すると位相が90度遅れる。
→三角関数を微分すると位相が90度進むこと
三角関数の積和公式
-
sinAcosB=21{sin(A+B)+sin(A−B)}
-
sinAsinB=21{−cos(A+B)+cos(A−B)}
-
cosAcosB=21{cos(A+B)+cos(A−B)}
→積和公式の導出と覚え方
三角関数の還元公式
〜 90∘−θ(余角)の公式〜
- sin(90∘−θ)=cosθ
- cos(90∘−θ)=sinθ
- tan(90∘−θ)=tanθ1
〜 90∘+θ の公式〜
- sin(90∘+θ)=cosθ
- cos(90∘+θ)=−sinθ
- tan(90∘+θ)=−tanθ1
〜 180∘−θ(補角)の公式〜
- sin(180∘−θ)=sinθ
- cos(180∘−θ)=−cosθ
- tan(180∘−θ)=−tanθ
〜 180∘+θ の公式〜
- sin(180∘+θ)=−sinθ
- cos(180∘+θ)=−cosθ
- tan(180∘+θ)=tanθ
〜 360∘+θ の公式〜
- sin(360∘+θ)=sinθ
- cos(360∘+θ)=cosθ
- tan(360∘+θ)=tanθ
〜−θ(負角)の公式〜
- sin(−θ)=−sinθ
- cos(−θ)=cosθ
- tan(−θ)=−tanθ
→90°+θ,180°+θなどの三角比の公式と覚え方
2倍角の公式
2倍角の公式は,2θ の三角関数を θ の三角関数で表す以下の公式です。

→2倍角の公式とその証明
三角関数の相互関係
-
sin2θ+cos2θ=1
-
tanθ=cosθsinθ
-
1+tan2θ=cos2θ1
-
1+tan2θ1=sin2θ1
→三角関数の相互関係とその証明
y=tan x のグラフ
y=tanx
のグラフは図のようになる。
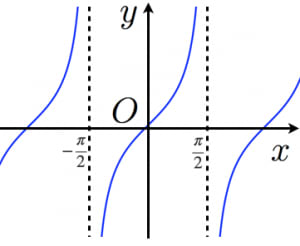
→y=tanxのグラフといろいろな性質
タンジェントの加法定理
tan(α+β)=1−tanαtanβtanα+tanβ
tan(α−β)=1+tanαtanβtanα−tanβ
(ただし,tan
の中身が全て
2π
の奇数倍にならないものとする)
→タンジェントの加法定理とその拡張
三角関数の微分公式(導関数)
- (sinx)′=cosx
- (cosx)′=−sinx
- (tanx)′=cos2x1
→三角関数の微分公式と問題例
OA=ba=⎝⎛a1a2a3⎠⎞, OB=b=⎝⎛b1b2b3⎠⎞
としたとき,三角形 OAB の面積 S は以下のように表せる。
-
S=21∥ba∥2∥b∥2−(ba⋅b)2
-
S=21(a2b3−a3b2)2+(a3b1−b3a1)2+(a1b2−a2b1)2
→三角形の面積のベクトル・成分を用いた公式
三角方程式
三角方程式とは,
cosθ=22
ような三角関数を含む方程式のことです。
→三角方程式の解き方
定理
円周上にある3点 A,B,C を頂点とする三角形 ABC について,1辺が円の直径と一致するなら,ABC は直角三角形。
→直角三角形の定義とさまざまな公式
単位円の定義
単位円とは,原点を中心とする半径1の円のこと。
→単位円の意味・三角比との関係
ここまでのまとめ
- y=sinx,y=cosx,y=tanx のグラフの形は覚える
- y=sinx と y=cosx は同じ形で,片方を 2π 平行移動すると重なる
- y=sinx と y=cosx の周期は 2π,y=tanx の周期は π
→三角関数のグラフの特徴と簡単な書き方
余弦定理
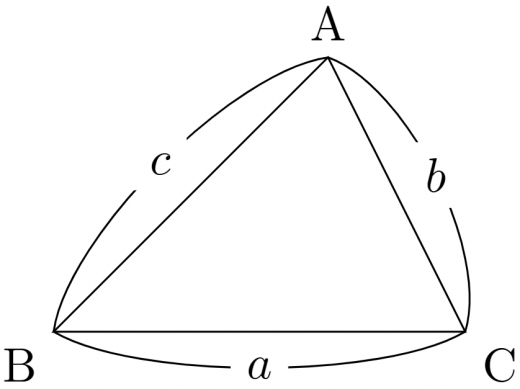
三角形 ABC において,
a2=b2+c2−2bccosAb2=c2+a2−2cacosBc2=a2+b2−2abcosC
が成り立つ。
なお,頂点 A に対応する角を A,頂点 B に対応する角を B,頂点 C に対応する角を C としている。
→余弦定理とその証明
sin, cos, tan とは
(図のように θ を含む直角三角形を描いたもとで)
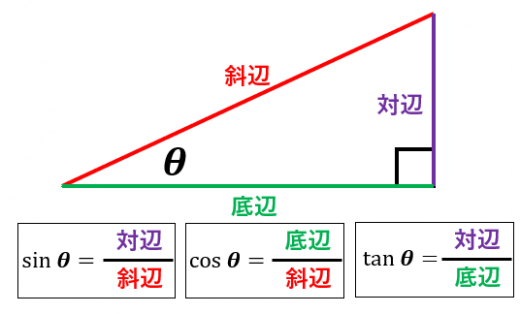
- sinθ とは 対辺の長さ/斜辺の長さ のこと
- cosθ とは 底辺の長さ/斜辺の長さ のこと
- tanθ とは 対辺の長さ/底辺の長さ のこと
→sin、cos、tan の意味
2倍角の公式
半角の公式は,2θ の三角関数を θ の三角関数で表す公式:
sin22θcos22θtan22θ=21−cosθ=21+cosθ=1+cosθ1−cosθ
→半角の公式
四倍角の公式は加法定理から導ける。オイラーの公式(ド・モアブルの定理)からも導ける。
→四倍角の公式の証明と考察
三角関数の定義1
0<θ<90∘ を満たす θ に対して
∠A=θ,∠B=90∘
となる直角三角形を描き,
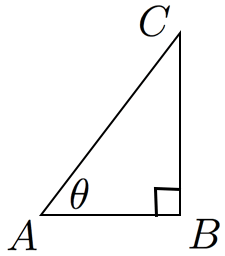
sinθ=ACBC,cosθ=ACAB,tanθ=ABBC
と定義する。
→三角関数の4通りの定義とメリットデメリット
弧度法
弧度法とは「半径が 1 で弧の長さが L である扇形の中心角を L ラジアンとする」ような角度の表し方。
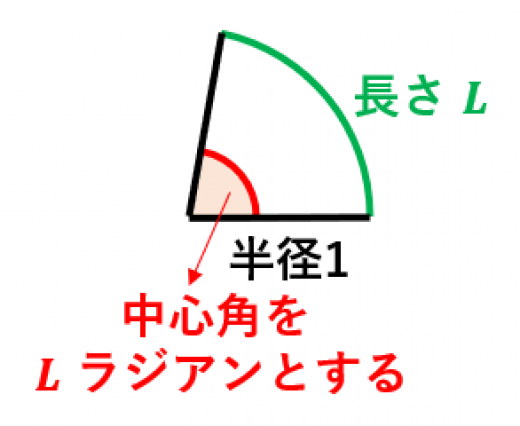
→弧度法の意味と度数法に対するメリット
正接定理
三角形
ABC
において,
tan2A+Btan2A−B=a+ba−b
→正接定理とその証明
問題
サイコロを3回振り,出た目を順に a,b,c とする。S=sinaπsinbπcoscπ とおく。
(1) 2⋅5π=π−3⋅5π を用いることで sin5π を求めよ。
(2) S=0 となる確率を求めよ。
(3) S が整数となる確率を求めよ。
(4) S が有理数となる確率を求めよ。
→三角関数分野:練習問題一覧|入試数学コンテスト過去問集
三角関数の和積公式
sinA+sinB=2sin2A+Bcos2A−B
sinA−sinB=2cos2A+Bsin2A−B
cosA+cosB=2cos2A+Bcos2A−B
cosA−cosB=−2sin2A+Bsin2A−B
→和積公式の覚え方と証明:覚えるべきか毎回導出すべきか?
置換積分の公式(不定積分)
x=g(t) と置換すると,
∫f(x)dx=∫f(g(t))dtdxdt
である。
→三角関数に関する置換積分3パターン
18∘ の三角比は
sin18∘cos18∘tan18∘=45−1=410+25=5+251
である。
→sin18°、cos18°、tan18°【覚えておくと便利な三角比】
(i) sinx≤x(x≥0)
(ii) cosx≥1−2x2(x∈R)
(iii)
sinx≥x−6x3(x≥0)
(iiii)
cosx≤1−2x2+24x4(x∈R)
→マクローリン展開にまつわる三角関数の不等式
定理1(チェビシェフ多項式)
cosnθ は cosθ の n 次多項式で表せる。
→チェビシェフ多項式
ラグランジュの三角恒等式(Lagrange's trigonometric identities)
(位相が等差数列なら)三角関数の和を計算できる:
k=0∑nsin(θ+kϕ)=sin2ϕsin(2(n+1)ϕ)sin(θ+2nϕ)k=0∑ncos(θ+kϕ)=sin2ϕsin(2(n+1)ϕ)cos(θ+2nϕ)
→位相が等差数列である三角関数の和の公式
tan1∘
は有理数か?
→tan1°、sin1°、cos1°が無理数であることの証明
逆三角関数
逆三角関数(Arcsin,Arccos,Arctan)とは,三角関数 sinx,cosx,tanx の逆関数のことです。
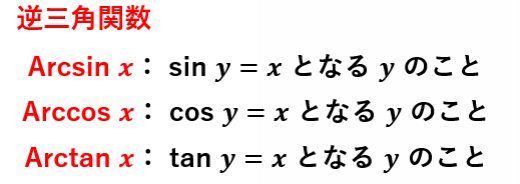
→逆三角関数(Arcsin,Arccos,Arctan)の意味と性質
京都大学理系数学 2023 大問6
p を 3 以上の素数,θ を実数とする。
- cos3θ と cos4θ を cosθ の式として表せ。
- cosθ=p1 のとき,θ=nm⋅π となるような正の整数 m,n が存在するか否かを理由を付けて説明せよ。
→京大2023大問6とチェビシェフ多項式
問題(防衛医科2024)
△ABC があり ∠A=185π,∠B=95π,∠C=6π である。辺 BC 上に ∠BAD=6π を取り B から辺 AC に下した垂線との交点を H とし BH と AD の交点を E とする。
- tan3πtan94πtan185πtan187π を求めよ。
- ∠CEH を求めよ。
→tan を用いた図形の問題~防衛医科2024から
(i)
A+B+C=π
のとき
tanA+tanB+tanC=tanAtanBtanC
(ii)
α+β+γ=2π
のとき
tanα1+tanβ1+tanγ1=tanαtanβtanγ1
(iii)
A+B+C=π
のとき
tanA1+tanB1+tanC1=4Sa2+b2+c2
→タンジェントの美しい関係式(tanA+tanB+tanC=tanAtanBtanC)
三倍角の公式
sin3θ=−4sin3θ+3sinθ
cos3θ=4cos3θ−3cosθ

→三倍角の公式:基礎からおもしろい発展形まで
内接円の半径と外接円の半径の関係
三角形
ABC
の内接円の半径を
r, 外接円の半径を
R
とするとき,
- r=4Rsin2Asin2Bsin2C
- R≧2r(オイラーの不等式)
→外接円の半径と内接円の半径の関係
三角形の内角における和積・積和公式
A+B+C=π
のとき以下が成立する:
-
sin 和積:
sinA+sinB+sinC=4cos2Acos2Bcos2C
-
sin 積和:
sinAsinBsinC=41(sin2A+sin2B+sin2C)
-
cos 和積:
cosA+cosB+cosC=4sin2Asin2Bsin2C+1
-
cos 積和:
cosAcosBcosC=−41(cos2A+cos2B+cos2C+1)
→三角形の内角における和積公式
オイラーの公式
n=1∏∞cos(2nx)=cos2xcos4xcos8x⋯=xsinx
→ヴィエトの無限積の公式
フーリエ変換
可積分関数 f(x) のフーリエ変換(Fourier transform)f^(ξ) を
f^(ξ)=∫−∞∞f(x)e−ixξdx
と定める(可積分関数とは ∫−∞∞∣f(x)∣dx<∞ を満たす関数のこと)。
→フーリエ変換の意味と応用例
三角関数の基本極限公式
x→0limxsinx=1x→0limx21−cosx=21x→0limxtanx=1
→三角関数 (sin,cos,tan) の極限まとめ