単位円の意味・三角比との関係
この記事では単位円の意味・使い方と,単位円と三角比の関係について解説します。
単位円の意味とグラフ
単位円の意味とグラフ
単位円とは,原点を中心とする半径1の円のこと。
平面上に単位円を描いてみましょう。
軸と で交わり, 軸と で交わります。
単位円を用いた三角比の定義
単位円を用いた三角比の定義
単位円を用いて三角比・三角関数()が定義されます。
単位円上で, から反時計回りに 回転した点を とする。このとき,
とする。

単位円の基本的な性質として
- は点 の 座標であること
- は点 の 座標であること
をおさえておきましょう。
さらに,直線 の傾きが です。
直角三角形を用いた三角比の定義との関係も理解しておきましょう。三角関数の3通りの定義とメリットデメリット
有名角の三角比と単位円
有名角の三角比と単位円
以下の有名角の三角比は,すべて重要です。
| 有名角 | ||
|---|---|---|
しかし,この有名角の三角比を全て丸暗記するのは大変です。そこで,以下の例題の解答のように単位円を考えて素早く導出できるようになるとよいです。
次の三角比の値を求めなさい。
(1)
(2)
(3)
(4)
(5)
有名角に対応する点を単位円上にプロットしてみます。
 (1) に対応する点の 座標が である。 の直角三角形を考えると, となる。
(1) に対応する点の 座標が である。 の直角三角形を考えると, となる。
(2) は と 軸について対称であるから に対応する点の 座標が である。 の直角三角形を考えると, となる。
(3)
(4)
(5)
答えを見ずに,単位円をもとに三角比の表をかいてみると良い練習になります!
三角関数の還元公式
三角関数の還元公式
三角関数の還元公式については別の記事で紹介していますが,単位円による定義から素早く導出できるとよいです。
次の三角比を, のみを使って表しなさい。
(1)
(2)
(3)

角度が のときの直角三角形と比べると, のときの直角三角形は 軸について対称です。
つまり
(1) 座標は 倍されるので,
(2) 座標はそのままなので,
(3) 傾きは 倍されるので,
次の三角比を, のみを使って表しなさい。
(1)
(2)
(3)
 例題1と同じように角度が のときの直角三角形と比べると, のときの直角三角形は 軸について対称であり, のときの直角三角形は原点について対称です。
例題1と同じように角度が のときの直角三角形と比べると, のときの直角三角形は 軸について対称であり, のときの直角三角形は原点について対称です。
つまり答えは
(1)
(2)
(3)
(複号同順)
次の三角比を, のみを使って表しなさい。
(1)
(2)
(3)
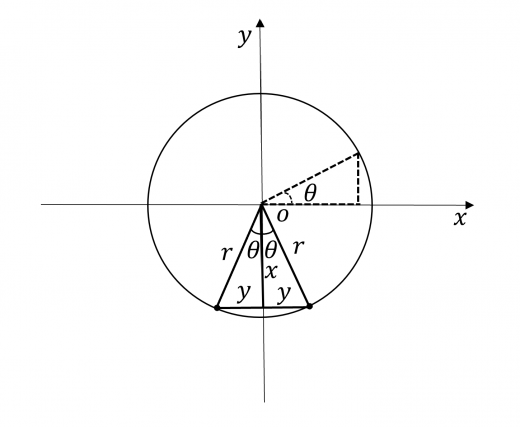
同様に考えると,答えは
(1)
(2)
(3)
(複号同順)
こちらも先ほどの三角比の有名角と同様に一瞬でわかるようになるまで繰り返し練習しましょう。
単位円に慣れることが,三角比や三角関数を得意にするための第一歩です。










