三角関数の4通りの定義とメリットデメリット
三角関数 はいろいろな分野に現れるとても重要な関数です。この記事では,三角関数の定義を3通り説明します。
直角三角形による定義
直角三角形による定義
まずは,1つめの定義です。直角三角形の辺の長さを使って三角関数(三角比)を定義します。
を満たす に対して
となる直角三角形を描き,
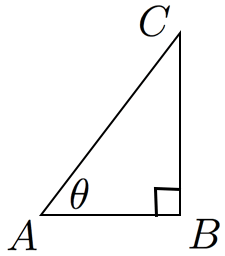
,, と定義する。
メリット
- 理解しやすい,「図形の計算を簡単にしたい」というモチベーションが分かりやすい。
- 正弦定理や余弦定理,面積公式などの有用な定理を理解するだけならこの定義で十分。
デメリット
- でしか定義できない(少し頑張っても まで)。
単位円による定義
単位円による定義
次は,単位円による三角関数の定義です。これは確実に覚えておきましょう。
任意の実数 に対して
軸の正の部分を原点中心に反時計回りに だけ回転させた半直線と単位円の交点の座標を と定義する。

また( のもとで), と定義する。
の範囲では,さきほどの直角三角形による定義と一致します。
メリット
- 任意の実数で三角関数が定義されたおかげで,図形問題以外にも使える道具となった。
- 例えば,一見三角関数と関係ないような無限級数の値を求めるのに使える。ウォリスの公式とその2通りの証明
- その他にも,フーリエ解析(信号処理論),特殊関数論など様々な分野で活躍できる。
デメリット
- (多くの初学者にとって)直角三角形による定義より分かりにくい。
- フーリエ解析などは高校で習わないので,定義の必要性を実感するのには時間がかかる。
発展:解析的な定義
発展:解析的な定義
マクローリン展開による定義
次は,マクローリン展開(テイラー展開)による定義です。三角関数は実数だけでなく,複素数に対しても定義できます。
任意の複素数 に対して
実数の範囲では単位円による定義と一致します。
メリット
- 複素数でも定義されるのでスッキリして美しい。
- 「角度」という概念を介さずに三角関数が定義できる。
デメリット
- 無限級数による定義であるため,本質的に収束性の議論が必要である。
- 高校生にとってはとても難しい,必要ない。
微分方程式による定義
最後に微分方程式を用いた定義を紹介します。
二階線型微分方程式 の解のうち,初期値 を満たすものを , を満たすものを と定義する。
メリット
- 単振動といった物理的意味と直結している。
- 微分方程式の解の一意性を通して様々な公式(加法定理など)が証明される。
デメリット
- 高校生にとってはとても難しい,必要ない。
終わりに
終わりに
解析的な定義を高校数学で使うことはありませんが,定義2まではきちんと覚えておきましょう!
1999年東大入試で三角関数の定義が出題されています。
三角関数は図形問題にはもちろんのこといろいろな分野に登場する重要な関数です。以下,三角関数の定義を3通り解説しますが2つめまでは理解して自分でも説明できるようになっておきましょう。











