二次曲線 に関する19記事をまとめました。くわしくは各リンク先を見てください。
楕円の面積公式
楕円の面積 S は,
円周率×長半径×短半径
で計算できる。つまり,S=πab

→楕円の面積公式の3通りの導出
直線 l と点 P からの距離が等しい点の集合は放物線である。l をこの放物線の準線,P を焦点と呼ぶ。
→放物線の準線・焦点と一般化
双曲線の漸近線
-
パターン1.双曲線 a2x2−b2y2=1 の漸近線は y=±abx
-
パターン2.双曲線
a2x2−b2y2=−1
の漸近線も
y=±abx
→双曲線の漸近線の簡単な求め方と証明
楕円の接線を求める公式(原点中心の場合)
楕円
a2x2+b2y2=1
上の点
P(x0,y0)
における接線の方程式は,
a2x0x+b2y0y=1
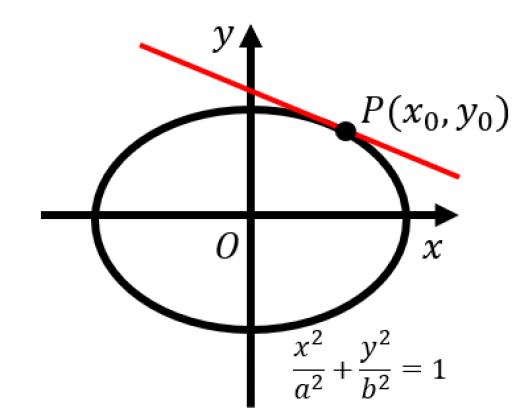
→楕円の接線を求める公式とその証明
離心率とは
点 F からの距離と直線 l からの距離の比が一定である点 P の軌跡は二次曲線になる。この比のことを離心率と呼ぶ。

→離心率の意味と関連する計算
円:x2+y2=r2 の媒介変数表示として,
- x=rcosθ,y=rsinθ
- x=r⋅1+t21−t2,y=r⋅1+t22t
- x=coshϕr,y=rtanhϕ
がある。
→楕円・双曲線の媒介変数表示の3通りの方法
双曲線とは
2点からの距離の差が一定である点の軌跡を双曲線と言う。また,この2点のことを焦点と言う。

→双曲線
楕円とは
2点からの距離の和が一定である点の軌跡を楕円と言う。また,この2点のことを焦点という。
楕円の端を結ぶ直線のうち,長いものを 長軸,短いものを 短軸 という。
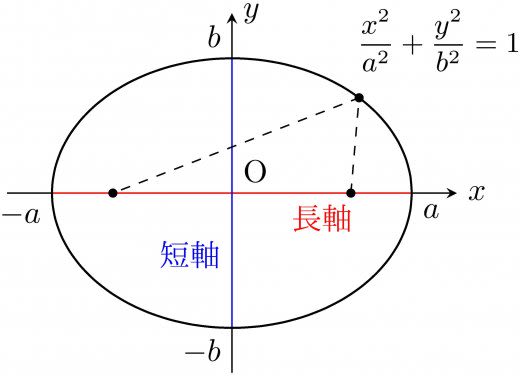
→楕円
→全ての放物線が相似であることの証明
1. 円錐曲線の切る角度による分類
- 平面が母線より緩いとき楕円
- 平面が母線より急なとき双曲線
- 平面が母線と平行なとき放物線
→二次曲線の分類(四通りの方法)
定理
パラボラアンテナの対称軸に対して平行に入射した信号は「焦点に」「同時に」届く。
→パラボラアンテナの原理と放物線の性質
準円

二次曲線に対して,二本の直交する接線が引けるような点の軌跡は円である。これを二次曲線の準円と言う。
→楕円,放物線,双曲線の準円
r=1+εcosθl
(l>0,ε≧0)は二次曲線を表す。
→二次曲線(楕円,放物線,双曲線)の極座標表示
二本の漸近線が直交するような双曲線を,直角双曲線と言う。
- 二次曲線:x2−y2=a(a=0)
は直角双曲線である。
- 反比例:xy=k
も直角双曲線である。
→直角双曲線の方程式と性質
斜めの楕円の方程式
-
原点を中心とする楕円は,
Ax2+2Bxy+Cy2=1
ただし A>0,C>0,AC−B2>0
という方程式で表せる。
-
逆に,上記の方程式は原点を中心とする楕円を表す。
→斜めの楕円の方程式(特に45度回転)
楕円の反射定理
楕円の焦点から出た光は,反射してから反対側の焦点を通る。
→楕円の反射定理とその証明
楕円積分(ルジャンドルの標準形)
-
E(k,ϕ)=∫0ϕ1−k2sin2θdθ
のことを第二種楕円積分という。
-
F(k,ϕ)=∫0ϕ1−k2sin2θ1dθ
のことを第一種楕円積分という。
→楕円積分の意味と身近な4つの例
定義
レムニスケート曲線とは,極方程式 r2=a2cos2θ で表される曲線である。
しばしば連珠形ということもある。
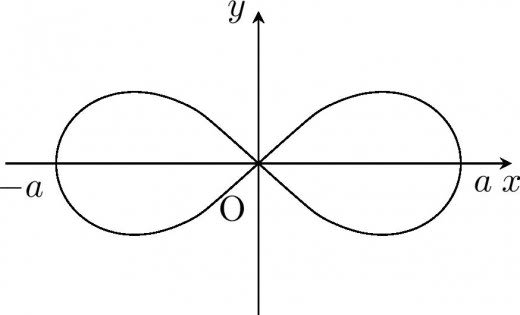
→レムニスケート曲線とその性質
楕円の周長
長軸の長さが
2a,短軸の長さが
2b
である楕円:
a2x2+b2y2=1
の周の長さは,
L=2πa(t=0∑∞ct21−2tϵ2t)
ただし,ϵ
は離心率で,ϵ2=1−a2b2
を満たし,
c0ct=1=(2t)!!(2t−1)!!=2t(2t−2)⋯2(2t−1)(2t−3)⋯1(t≥1)
→楕円の周の長さの求め方と近似公式












