斜めの楕円の方程式(特に45度回転)
-
原点を中心とする楕円は,
ただし
という方程式で表せる。 -
逆に,上記の方程式は原点を中心とする楕円を表す。
斜めの楕円の方程式の一般形について,上の二つの定理を証明し,特に45度回転の場合について考察します。
斜めの楕円
斜めの楕円
数学3で扱う楕円は主軸が , 軸方向であるようなもの: です。これを原点中心に回転させた斜めの楕円について考えてみます。
入試でもまれに斜めの楕円が登場します。特に, 回転させたもの( であるもの,詳細は後述)が頻出です。
という方程式は, より,冒頭の定理から楕円を表すことがわかる。
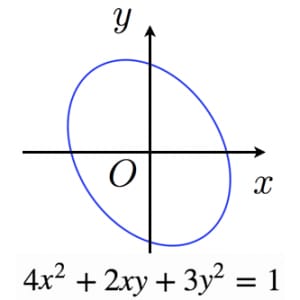
1の証明
1の証明
まずは,数学3で扱う「いつもの楕円」を回転させるとどうなるか計算することで1を証明します。
原点を中心とする一般の楕円は「いつもの楕円」 を適切に回転させることで得られる。
「いつもの楕円」を 回転させたものが を通るとすると,
となる。(計算過程は後述)
これは,整理すると という方程式になる。 などは簡単に確認できる。
複素数を用いた計算
複素数を用いることで,点の回転を計算できます。→ 複素数平面における極形式と回転
最近の教科書ではこの方法が主流となります。
を複素数平面上の点 だとみなす。
このとき, に を掛けた点が を 回転させた点となる。
逆に 回転させた点を とすると, となる。計算すると となるため, , となる。
行列を用いた計算
を掛けることによって点の回転を計算できます。→ 一次変換の意味と重要な5つの例(折り返し・回転・対称移動)
大学以降ではこの方法も頻繁に用いられます。旧課程では複素数の代わりにこの方法で回転を計算していました。
を 回転させた点を とおく。
よって,, となる。
2の証明
2の証明
こちらは少し大変です。高校数学のみで頑張って計算することもできますが,固有値,固有ベクトル,対称行列の性質,正定値行列の概念を用いるのがスマートです。
と定義すると, という方程式は, と書ける(二次形式の行列表現)。
ここで,条件より は正定値行列なので,ある直交行列(回転行列) を用いて ()と対角化できる。
これを用いると,上記の方程式は,
となる。
これは, による回転で に移ることを表している。つまり,いつもの楕円を原点中心に回転させたものである。
45度回転させた楕円の方程式
45度回転させた楕円の方程式
冒頭の式において,特に
いつもの楕円を 回転させたもの
いつもの楕円を 回転させたもの に関して折り返しても図形は変わらない
に注意する。
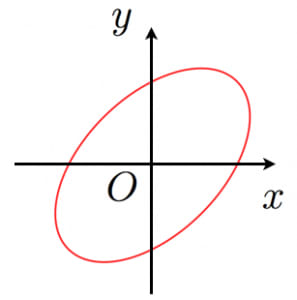
- のとき, と に関して対称な式となり, に関して折り返しても図形は変わらない。
- は を通るので, に関して折り返しても図形が変わらないとき, が必要である。
はいつもの楕円を45度回転した図形である(上の図の赤線の図形)。
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題249では,斜めの楕円に関する問題と3通りの解法を紹介しています。
固有値,固有ベクトルの考え方を使えば高次元の二次曲面についても議論できます!











