対称行列の定義と性質~固有値と固有ベクトルの性質
更新
行列 が対称行列であるとは,転置しても変わらないことをいう。
つまり, の 行 列の成分を としたとき, が成立する行列のことをいう。
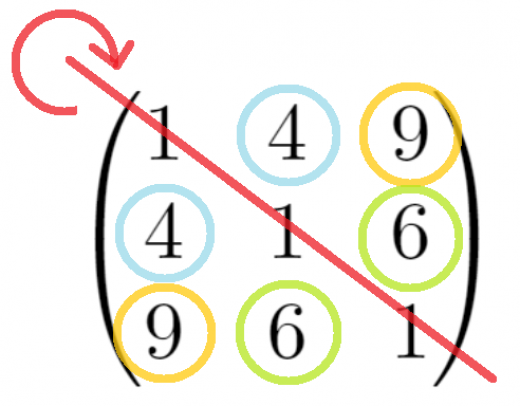
この記事では対称行列とその性質を解説します。線型代数で頻繁に登場する概念なのでマスターしましょう!
対称行列と固有値・固有ベクトル
対称行列と固有値・固有ベクトル
任意の実対称行列 について,
- 固有値は実数である
- 異なる固有値に対応する固有ベクトルは直交する
対称行列の重要な2つの性質を証明します。
具体例
証明の前にまずは具体例からです。
固有値と固有ベクトルの定義,求め方については固有値,固有ベクトルの定義と具体的な計算方法を参照して下さい。
の固有値と固有ベクトルを求めよ。
固有方程式は なので,固有値は
に対応する固有ベクトルは
に対応する固有ベクトルは
固有値は実数で,2本の固有ベクトルは直交している!
固有値が実数であることの証明
の1つの固有値を ,対応する固有ベクトルを とおく。
- 固有値,固有ベクトルの定義より
- 両辺の共役転置を取ると
ここで,二次形式 について二通りの変形をする。
- 1つ目の式より,
- 2つ目の式より,
以上から
固有ベクトルの定義より は ベクトルではないので
よって となる。つまり は実数。
補足:
- は のノルム(長さ)。つまり各成分の二乗和のルート。
- は の共役転置。が成立する。実対称行列については
固有ベクトルが直交することの証明
の固有値 に対応する固有ベクトルを , に対応する固有ベクトルを とおく:
2つ目の式の共役転置を取る
ここで,二次形式 について2通りの変形をする。
- についての式より,
- についての式より,
よって,
のとき となり と は直交する。
注:この定理をもとに「対称行列は直交行列で対角化できる」という非常に重要な定理を証明できます。対称行列はいろいろなところに登場する&固有値,固有ベクトルに関して美しい理論があるため大事です。
交代行列との関連
交代行列との関連
行列の「分解」
「対称行列は偶関数のようなもの」「交代行列は奇関数のようなもの」といえます。
特に次の定理が成立します。
任意の実数係数行列は 対称行列と交代行列の和で表される。
行列 に対して は対称行列, は交代行列である。
より題意は示された。
二つの定理の証明が似ているのもおもしろいです。











