行列のランク(rank)の8通りの同値な定義・性質
更新
任意の行列に対してランク(rank)と呼ばれる重要な量が定まる。ランクにはいろいろな意味(性質)がある。
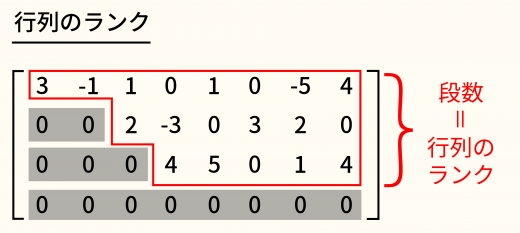
ランクには様々な意味がある
ランクには様々な意味がある
ランク(階数,rank)とは任意の(正方行列とは限らない)行列に対して定義される重要な量です。
ランクには同値な定義(性質)がたくさんあります。以下の1〜8のいずれか一つをランクの定義とすれば,残りはランクの性質として導けます。
8つとも重要です。全て理解するのが理想ですが,まずは自分が親しみやすい定義を一つきちんと覚えましょう。
ランクの定義,性質(一次独立編)
ランクの定義,性質(一次独立編)
1. の正則(行列式が0でない)な小行列でサイズが最大なもののサイズ
例えば について, の部分行列の一つ は正則ですが, の部分行列は全て非正則です。よって です。
2. の一次独立な行ベクトルの最大本数
さきほどの例:一行目 と二行目 は一次独立ですが,三行目 を加えると一次従属になる(二行目の 倍から一行目の 倍を引くと三行目になる)ので です。
3. の一次独立な列ベクトルの最大本数
さきほどの例:一列目 と三列目 は一次独立ですが,どの三列を選んでも一次従属になるので です。
ランクの定義,性質(行列の変形編)
ランクの定義,性質(行列の変形編)
4.階段形にしたときに でない成分が残る行の数
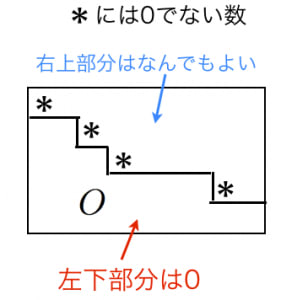
階段形とは図のような行列です。任意の行列 に対して正則行列 をうまく取ってくれば を階段形にできます。
さきほどの例: とすれば となるので です。
実際にランクを計算するときは4を使います。
5.ランク標準形にしたときに が並ぶ数
任意の行列 に対して正則行列 をうまく取ってくれば という形にできます( は適切なサイズの単位行列)。このときの のサイズ(一意に決まる)が のランクとなります。
さきほどの例: , とすれば となるので です。
ランクの定義,性質(その他編)
ランクの定義,性質(その他編)
6. ,つまり の像の次元
さきほどの例: の像は実数 を用いて と表される点の集合です。これは実は三次元空間内の二次元平面 (で表される平面)を表しているので です。
7. の でない特異値の数( の でない固有値の数)
注: の 「 でない固有値の数」はランクと等しいとは限りません。例えば の固有値は が2つ(つまり「 でない固有値の数」は )ですが,ランクは です。
8.以下の条件を満たす最小の
条件: 本の縦ベクトル が存在して と書ける。
注: は縦ベクトルと横ベクトルの積なので行列です。
行列のランクの計算例
行列のランクの計算例
定義4を使ってランクを計算してみましょう。つまり,階段形にしたときに でない成分が残る行の数を計算します。
行基本変形は正則行列を左からかけることに対応するので,行基本変形を行なって階段形にできれば,ランクを求めることができます。
とする。 を求めよ。
よって,
- つまり のとき
- のとき
行列の基本変形の意味と応用(rank・行列式の計算)にも,ランクの求め方が載っています。合わせてご覧ください。
ちなみに8で を非負ベクトルに限定したものを行列の非負ランクと言います。
Tag:数検1級の範囲と必要な公式まとめ











