行列の基本変形の意味と応用(rank・行列式の計算)
更新
行基本変形とは,行の交換,行の定数倍,他の行に定数倍を加えるという3つの操作のことです。
この記事では,行列の基本変形,特に行基本変形について,意味と応用をわかりやすく説明します。
行基本変形とは
行基本変形とは
行列に対する以下の3つの操作を行基本変形と言います。
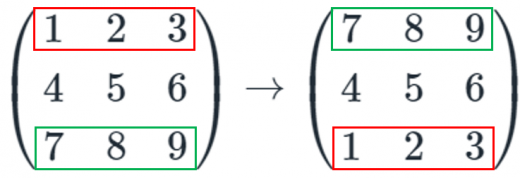
ある行と別の行を交換する。
例. 1行目と3行目を交換する
ある行を定数倍する。
例. 3行目を2倍する

ある行の定数倍を別の行に加える(または引く)。
例. 1行目の2倍を3行目から引く

行基本変形とランク(rank)
行基本変形とランク(rank)
行基本変形を使えば,与えられた行列 の rank を計算できます。
-
行基本変形を繰り返して,図のような階段形にする。

-
このとき, でない成分がある行の数が の rank となる。
階段形にする方法や,ランクを計算する例題は行列のランク(rank)の8通りの同値な定義・性質の記事末をどうぞ。
- 行基本変形は,左から正則行列をかけることに対応する(後述の定理1)。
- 正則行列をかけてもrankは変わらないので,得られる階段形の行列のrankはもとの行列のrankと一致する。
- 階段形の行列のrankは一瞬で求まる( でない成分がある行の数)。
行基本変形と行列式
行基本変形と行列式
行列式の計算でも行基本変形が活躍します。
- 行基本変形のうち操作1と操作3を繰り返して,階段形にする。
- 得られた階段形の対角成分の積に,「操作1の回数」をかける。
※操作2(定数倍)を使わずに階段形にすることで計算が楽になります。
与えられた正方行列 に対して行基本変形を繰り返すことで階段形 (上三角行列)にする。これは,適当な正則行列 を左からかけることに対応する(→後述の定理1)。
つまり,
よって, であり,
- は対角成分の積で簡単に求まる
- も変形の過程を見れば分かる( を操作1の回数だけかける)
ので が求まる。
行基本変形の他の応用
行基本変形の他の応用
行基本変形は,rank や行列式を計算するのに役立ちましたが,他にも応用例はあります。
逆行列を求める
行基本変形を使って逆行列を計算できます。 に行基本変形をして にしたとき, が の逆行列になります。詳細は 逆行列の定義・逆行列を求める2通りの方法と例題 の「逆行列の求め方1」で解説しています。
連立方程式の解を求める
行基本変形は連立方程式を解くときにも活躍します。ガウスの消去法(掃き出し法)と呼ばれます。連立方程式が解ければ,行列の核(カーネル)も計算できます。
行基本変形と正則行列
行基本変形と正則行列
行基本変形は正則行列を左からかけることに対応する。
操作1から操作3まで順に確認していきます。
操作1(行の交換)
行目と 行目の交換は,単位行列の 行目と 行目を交換した行列 を左からかけることに対応します。
に左から をかけると, となり1行目と3行目が交換された。
なお, の行列式は なので正則です。
操作2(定数倍)
行目を 倍する操作は,単位行列の 成分を とした行列 を左からかけることに対応します。
に左から をかけると, となり3行目が2倍された。
なお, の行列式は なので, のもとで正則です。
操作3(定数倍を加える)
行目の 倍を 行目に加える操作は,単位行列の 成分を とした行列 を左からかけることに対応します。
に左から をかけると, となり1行目の2倍が3行目から引かれた。
なお, の行列式は なので正則です。
正則行列について,詳しくは 行列が正則であることの意味と5つの条件 をご覧ください。
行基本変形は正則行列の掛け算で表される
- 行基本変形の3つの操作は全て,ある正則行列をかけることで実現できます。
- 正則行列の積は正則行列です。
以上より,行基本変形を繰り返す操作は,ある正則行列をかけることで実現できることがわかります。
列基本変形とは
列基本変形とは
行の場合と同様に,以下の三つの操作を列基本変形と言います。
操作1: 列目と 列目を交換する
操作2: 列目を 倍する()
操作3: 列目の 倍を 列目に加える
列基本変形は正則行列を右からかけることに対応します。(行基本変形の場合と同様に説明できます)
私は4×4以上の行列式やrankを手計算で求めるのがいやなので計算機を使います。











