微分 に関する46記事をまとめました。くわしくは各リンク先を見てください。
この記事では合成関数を微分する方法を2通り紹介します。合成関数の微分をマスターすれば y=(x2+3x+1)4 など複雑な関数も微分できます。例題7問と3通りの証明も解説します。

→合成関数の微分公式と例題7問
連続,微分可能の大雑把な意味
- 連続とは,関数のグラフがつながっていること。
- 微分可能とは,関数のグラフが滑らかであること。
→関数の連続性と微分可能性の意味と関係
商の微分公式
{g(x)f(x)}′={g(x)}2f′(x)g(x)−f(x)g′(x)
→商の微分公式をわかりやすく【例題・証明・覚え方】
→微分公式一覧(基礎から発展まで)
指数関数の微分
任意の
a>0
に対して
y=ax の導関数は,y′=axloga である。
→指数関数y=a^xの微分公式の4通りの証明
サインの微分公式
(sinx)′=cosx

→sinxの微分公式の3通りの証明
コサインの微分
y=cosx の導関数は,y′=−sinx
→cosxの微分公式のいろいろな証明
公式1
任意の正の整数
n
に対し,(xn)′=nxn−1
→べき関数(y=x^n)の微分公式の3通りの証明
極大の意味

- 極大(きょくだい)とは,近所で一番大きいことを表す。
- 最大とは,全体で一番大きいことを表す。
→極大値・極小値の意味と求め方
タンジェントの微分
y=tanx の導関数は,y′=cos2x1
→tanxと1/tan xの微分公式のいろいろな証明
増減表とは,それぞれの区間で 関数 f(x) が増加するか減少するかなどを表した表のことです。

→増減表の書き方
微分係数と導関数の意味を確認した後,いろいろな関数の導関数を計算します。導関数の計算で高校数学の総復習ができます。
→導関数の意味といろいろな例
三角関数の微分公式(導関数)
- (sinx)′=cosx
- (cosx)′=−sinx
- (tanx)′=cos2x1
→三角関数の微分公式と問題例
微分係数の定義
f′(a)=h→0limhf(a+h)−f(a)
→微分係数の定義
微分の定義
f′(x)=h→0limhf(x+h)−f(x)
→分数関数の微分公式(商の微分)とその証明・計算例
ジョルダンの不等式
0≤x≤2π
において,
π2x≤sinx≤x
→ジョルダンの不等式とその3通りの証明
サイクロイド曲線
媒介変数
θ
を用いて
x(θ)=a(θ−sinθ)
y(θ)=a(1−cosθ)
と表される曲線をサイクロイド(Cycloid)と呼ぶ。
→サイクロイドについて覚えておくべきこと
対数微分法とは,両辺の対数を取ってから微分する方法のこと。
例えば「xx の微分」で活躍する。

→対数微分法のやり方と例題~x^x の微分
積の微分公式
f(x),g(x)
が(考えている区間で)微分可能なとき
{f(x)g(x)}′=f′(x)g(x)+f(x)g′(x)
→積の微分公式とその証明の味わい
sin と cos のマクローリン展開
sinx=x−3!x3+5!x5−7!x7+⋯
cosx=1−2!x2+4!x4−6!x6+⋯
→sinとcosのn階微分とマクローリン展開
逆関数の微分公式
dydx=dxdy1
逆関数の微分は,もとの関数の微分の逆数
→逆関数の微分公式を例題と図で理解する
2曲線が接するとは(一般の場合)
y=f(x) と y=g(x) が x=a で接する
⟺ f(a)=g(a) かつ f′(a)=g′(a)
→2曲線が接する3通りの条件
連鎖律(チェインルール)
-
f(x,y) が全微分可能で x=x(t),y=y(t) が微分可能であるとき次が成り立つ。
dtdf=∂x∂fdtdx+∂y∂fdtdy
-
f(x,y) が全微分可能で x=x(u,v),y=y(u,v) が微分可能であるとき次が成り立つ。
∂x∂f=∂u∂f∂x∂u+∂v∂f∂x∂v∂y∂f=∂u∂f∂y∂u+∂v∂f∂y∂v
→連鎖律(chain rule)の練習問題
有名な関数のマクローリン展開
sinx=x−3!x3+5!x5−⋯
cosx=1−2!x2+4!x4−⋯
ex=1+x+2!x2+3!x3+⋯
log(1+x)=x−2x2+3x3−⋯
※ただし,log(1+x)
に関しては
−1<x≦1
でのみ成立する式です。
→マクローリン展開
ライプニッツの公式(Leibniz rule)
(fg)(n)=k=0∑nnCkf(k)g(n−k)
→ライプニッツの公式の証明と二項定理
ニュートン法(Newton’s method)とは,方程式の解を高速に計算するアルゴリズムである。
→ニュートン法の解説とそれを背景とする入試問題
方針
対数関数と1次関数の積なので,2階微分は扱いやすい式(有理式)になることが分かります。多少計算は大変ですが,見通しが立っているので安心して計算できます。
→微分を用いた不等式証明の問題
偏微分(へんびぶん)とは,多変数関数を「特定の文字以外定数とみなして」微分したもののことです。

→偏微分の意味と計算例・応用
有名な曲線たち
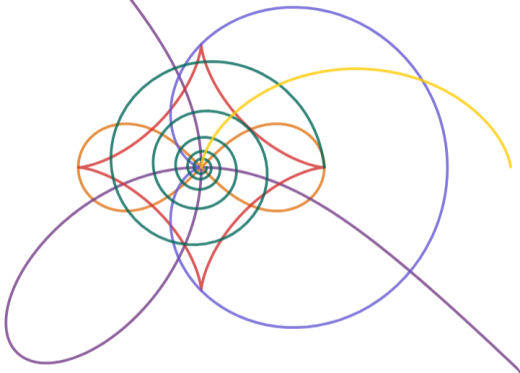
→媒介変数表示された有名な曲線7つ
定理
f(x)
が区間内で二階微分可能なとき,
- 下に凸
⟺
二階微分
f′′(x)≧0
- 上に凸
⟺
二階微分
f′′(x)≦0
→上に凸,下に凸な関数と二階微分
→曲率・曲率半径の感覚的な意味と求め方
Arctan のマクローリン展開
∣x∣≤1 なる実数 x について,
Arctanx=x−3x3+5x5−7x7+⋯
→Arctanのマクローリン展開の3通りの方法
平均値の定理(ラグランジュの平均値の定理)
a≦x≦b で微分可能な関数 f(x) に対して,
b−af(b)−f(a)=f′(c)
を満たす
c
が
a
と
b
の間に存在する。
→平均値の定理とは?意味・証明と入試応用例まで解説
対数関数のテイラー展開
−1<x≤1 のとき,
log(1+x)=x−2x2+3x3−4x4+⋯
→log xのn階微分とテイラー展開
一次近似
x≒a のとき,
f(x)≒f(a)+f′(a)(x−a)
→一次近似の意味とよく使う近似公式一覧
デカルトの葉線
xy
平面上において
x3+y3−3axy=0
で表される曲線をデカルトの葉線と言う。
→デカルトの葉線の漸近線と面積
サイクロイドと面積・体積・長さ
サイクロイド曲線 C:
{x=a(θ−sinθ)y=a(1−cosθ)
(a>0,0≦θ≦2π)について,
- C と x 軸で囲まれた部分の面積は 3πa2
- x 軸周りの回転体の体積は 5π2a3
- 長さは 8a
→サイクロイド曲線のグラフと面積・体積・長さ
対数平均の不等式
x,y>0 かつ x=y のとき,
xy<logx−logyx−y<2x+y
→対数平均に関する不等式の証明
伸開線の定義
曲線に対して,その曲線に巻きつけられた糸をたるませないようにほどいていくときに糸の端点が描く軌跡のことを伸開線(Involute)と言う。
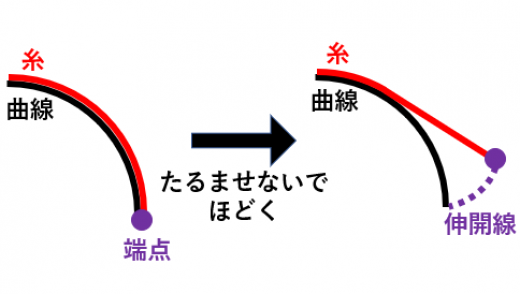
→伸開線(インボリュート)と縮閉線(エボリュート)の意味と計算例
この記事では覚えておくべきマクローリン展開の公式をまとめています。
→基本的なテイラー展開・マクローリン展開公式一覧
arcsin・arccos のマクローリン展開
∣x∣<1 なる実数 x について,
arcsinxarccosx=x+61x3+403x5+⋯=2π−x−61x3−403x5−⋯
となる。
→arcsin・arccos のマクローリン展開
東京大学理系数学2025年 第1問
座標平面上の点 A(0,0),B(0,1),C(1,1),D(1,0) を考える。実数 0<t<1 に対して,線分 AB,BC,CD を t:(1−t) に内分する点をそれぞれ Pt,Qt,Rt とし,線分 PtQt,QtRt を t:(1−t) に内分する点をそれぞれ St,Tt とする。さらに線分 StTt を t:(1−t) に内分する点を Ut とする。
- 点 Ut の座標を求めよ。
- t が 0≦t≦1 の範囲を動くときに点 Ut が描く曲線と,線分 AD で囲まれた部分の面積を求めよ。
- a を 0<a<1 を満たす実数とする。t が 0≦t≦a の範囲を動くときに点 Ut が描く曲線の長さを,a の多項式の形で求めよ。
→【解答・解説】東大理系数学2025 第1問~ベジェ曲線
一変数関数の最小値は,多くの場合微分を用いて求めることができる。
→指数関数の微分を用いる数オリの応用問題
tanx
のマクローリン展開(x=0
におけるテイラー展開)は
tanx=x+31x3+152x5+31517x7+⋯
→tanxの高階微分とマクローリン展開
定理
関数 f(x) が f(x)=n=0∑∞anxn と無限級数展開されているとする。
この級数の収束半径を r とすると,∣x∣<r のもとで項別微分・項別積分ができる:
f′(x)∫f(x)dx=n=1∑∞nanxn−1=n=0∑∞n+1anxn+1+C
→項別微分・項別積分
定義
スカラー t を変数とするベクトル a の微分を
dtda=h→0limha(t+h)−a(t)
と定義する。計算結果はベクトル。
→ベクトルの微分













