上に凸，下に凸な関数と二階微分

更新日時 2021/03/07

定理： $f(x)$ が区間内で二階微分可能なとき，

下に凸 $\iff$ 二階微分 $f''(x)\geq 0$

上に凸 $\iff$ 二階微分 $f''(x)\leq 0$

上に凸，下に凸な関数の性質と入試問題への応用例として京大の問題を解説します。

下に凸な関数の定義と性質
上に凸な関数の定義と性質
上に凸，下に凸な関数と二階微分
京大の入試問題

下に凸な関数の定義と性質
グラフ上の二点を結んだ線分が常にグラフの上側にあるような関数を下に凸な関数（または単に凸関数）と言います。
式で表すと，区間内の任意の x1,x2x_1, x_2x1​,x2​ と λ (0≤λ≤1)\lambda \:(0\leq \lambda\leq 1)λ(0≤λ≤1) に対して，
λf(x1)+(1−λ)f(x2)≥f(λx1+(1−λ)x2)\lambda f(x_1)+(1-\lambda)f(x_2)\geq f(\lambda x_1+(1-\lambda)x_2)λf(x1​)+(1−λ)f(x2​)≥f(λx1​+(1−λ)x2​) となります。
（左辺は関数のグラフ上の二点を 1−λ:λ1-\lambda:\lambda1−λ:λ に内分する点 AAA の yyy 座標で，右辺は xxx 座標が AAA と同じで関数上にある点の yyy 座標です)
下に凸な関数は最小値＝極小値が成立するので，最適化理論など工学的にも非常に重要な概念です。
入試問題では「二階微分が正であることを示す→下に凸な関数→よって上記の不等式を適用できる」という流れで使うことが多いです。特に λ=12\lambda=\dfrac{1}{2}λ=21​ とした式： 12(f(x1)+f(x2))≥f(x1+x22)\dfrac{1}{2}(f(x_1)+f(x_2))\geq f(\dfrac{x_1+x_2}{2})21​(f(x1​)+f(x2​))≥f(2x1​+x2​​) を使うことが多いです。

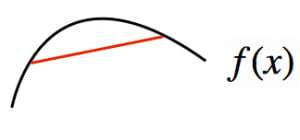
上に凸な関数の定義と性質
グラフ上の二点を結んだ線分が常にグラフの下側にあるような関数を上に凸な関数（または単に凹関数）と言います。
λf(x1)+(1−λ)f(x2)≤f(λx1+(1−λ)x2)\lambda f(x_1)+(1-\lambda)f(x_2)\leq f(\lambda x_1+(1-\lambda)x_2)λf(x1​)+(1−λ)f(x2​)≤f(λx1​+(1−λ)x2​) 
と不等号が逆向きになります。
「f(x)f(x)f(x) が上に凸   ⟺  \iff⟺ −f(x)-f(x)−f(x) が下に凸」が成立するので上に凸な関数と下に凸な関数は本質的に同じです。
下に凸と上に凸の見分け方：「凸」を「ボコっとしてる」と言い換えれば覚えやすいです。「下に凸は線分が上側」と覚えるのではなく「下にボコっとしてる」関数です。

上に凸，下に凸な関数と二階微分

二階微分が存在するとき，上に凸，下に凸の判定は二階微分の符号を見ればOKです。

下に凸 $\iff$ 二階微分 $f''(x)\geq 0$ の簡単な説明をします。

（説明）

下に凸

$\iff$ 線分が上側にある

$\iff$ 接線の傾きが減少しない

$\iff$ $f'(x)$ が広義単調増加（単調非減少）

$\iff$ $f''(x)\geq 0$

凸関数と二階微分の関係は有名な定理です。厳密な証明には平均値の定理などを使う必要がありますが，上記の方が直感的で分かりやすく，大雑把に理解するための説明としては十分だと思います。

京大の入試問題

凸関数の例題として1991年京大理系問4を解説します。ここまでの内容を理解していればかなり易しい問題です。

例題

実数 $a,b\:(0\leq a,\:b <\dfrac{\pi}{4})$ に対して以下の不等式を証明せよ：

$\sqrt{\tan a\tan b}\leq \tan (\dfrac{a+b}{2})\leq\dfrac{1}{2}(\tan a+\tan b)$

解答

・右側は $f(x)=\tan x$ に凸関数の定義である不等式を使うだけ。 $f(x)=\tan x$ が凸関数であることを示すために二階微分を計算する。

$f'(x)=(\cos x)^{-2},\:f''(x)=2(\cos x)^{-3}\sin x$ となり区間内で $f''(x)\geq 0$

よって凸関数の定義式で $\lambda=\dfrac{1}{2}$ として右側の不等式を得る。

・左側は対数を取ってから同様の議論をする。

まず， $a=0$ または $b=0$ のとき，最左辺は $0$ となり成立。

そうでないとき，両辺の対数を取ると示すべき不等式は，

$\dfrac{1}{2}\log\tan a+\dfrac{1}{2}\log\tan b\leq\log\tan\dfrac{a+b}{2}$

よって， $g(x)=\log\tan x$ が区間内で上に凸であることを証明すればよい。

二階微分を計算する：

$g'(x)=\tfrac{(\tan x)'}{\tan x}=\tfrac{1}{\sin x\cos x}=\tfrac{2}{\sin 2x}$

$g''(x)=\tfrac{-4\cos 2x}{\sin^2 2x}$

これは区間内で負となるのでOK。

なお，より発展的な話題としてイェンゼンの不等式があります。→イェンゼンの不等式の3通りの証明

凸関数の理論は奥が深く，凸解析という分野があるくらいです。

Tag:京大入試数学の良問と背景知識まとめ

Tag:数学3の教科書に載っている公式の解説一覧