物理 に関する18記事をまとめました。くわしくは各リンク先を見てください。
空気抵抗を考慮しない斜方投射において,一番遠くまで飛ばすには45度の角度で投げればよい。
→斜方投射の公式の導出と飛距離を伸ばす方法
水平線までの距離はだいたい4km〜5km
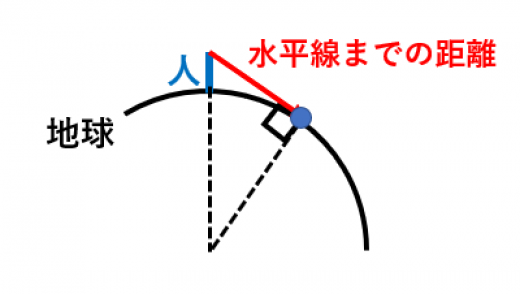
→水平線,地平線までの距離の計算方法と例
スネルの法則
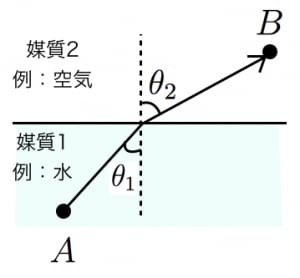
入射角と屈折角のサインの比は媒質中の光の速さの比と等しい:
sinθ2sinθ1=v2v1
→スネルの法則(屈折の法則)をフェルマーの原理を用いて証明
反発係数を考慮した自由落下の問題では,
- 衝突の回数は理論上無限大だが,
- 停止するまでにかかる時間
T
は有限:
T=g2h⋅1−e1+e
→反発係数を考慮した自由落下の有名問題
→運動量保存則とエネルギー保存則の導出
ポアソンの法則
理想気体の断熱変化において
pVγ=(一定)
ただし,γ
は比熱比と呼ばれる量であり,単原子分子理想気体では
35
→断熱変化におけるポアソンの式の導出
単振り子の周期
単振り子の周期は,
-
高校物理で習う近似解は 2πgl
-
厳密解は
4gl∫02π1−sin22θ0sin2ϕdϕ
→単振り子の周期(近似解と厳密解の比較)
二次元において運動方程式を極座標で記述すると,
m(r¨−rθ˙2)=Fr
mr1dtd(r2θ˙)=Fθ
→二次元極座標における運動方程式とその導出
地球は「焦点の1つが太陽であるような楕円軌道」を描く。
→地球の公転軌道が楕円であることの導出
質量が
M,半径が
R
の球の(中心を通る軸まわりの)慣性モーメントは
I=52MR2
→球の慣性モーメントの2通りの求め方
ナビエ-ストークス方程式
ρ{∂t∂v+(v⋅∇)v}=−∇p+μ∇2v+ρf
→ナビエ-ストークス方程式の導出
例題1
dtdx−3x=et+1
の一般解を求めよ。
→微分方程式の解法(同次形・線形微分方程式)
例題
次の連立微分方程式を解け。
⎩⎨⎧dtdx1(t)=x1(t)−2x2(t)dtdx2(t)=x1(t)+4x2(t)
ただし x1(0)=1,x2(0)=−2 とする。
→連立微分方程式の3通りの解き方
リッカチの微分方程式
dtdx=f(t)x2+g(t)x+h(t)
という形の微分方程式をリッカチ(Riccati)の微分方程式と言う。ただし f(t),g(t),h(t) は与えられた t の関数である。
→リッカチの微分方程式・ベルヌーイの微分方程式
定理
定数係数の n 階斉次線形微分方程式
dtndnx+an−1dtn−1dn−1x+⋯+a1dtdx+a0x=0⋯(i)
の解の集合は,n 次元のベクトル空間になる。
→n階斉次線形微分方程式の解空間
リプシッツ条件について解説します。リプシッツ条件は,
- 大雑把に言うと「出力の変動が,入力の変動の定数倍でおさえられる」という条件です。詳しくは後述します。
- 微分方程式の初期値問題を考えるときに重要な条件です。
- リプシッツ条件を満たせば,微分方程式の解が一意に定まるので嬉しいです。
→リプシッツ条件と微分方程式の解の一意性
東大数学科院試 2021から抜粋
初期値が x(1)=a,dtdx(1)=b となる微分方程式
dt2d2x−t22x=t2
の解 x(t) を求めよ。
ただし t は正の実数とする。
→微分方程式の例題(東大院2021から)
定義
関数 f(x) に対して
L[f](s)=∫0∞e−sxf(x)dx
という「s についての関数を返す変換」をラプラス変換という。
→ラプラス変換の定義と具体例・性質







