さて本題です。実はリッカチの微分方程式は,基本的に1つ特殊解が得られている状況でないと一般解を求められません。逆に,特殊解さえ分かっていれば一般解を求められます。
それでは解法です。
リッカチの微分方程式の解法
元の方程式の特殊解を x=u(t) とおく。与式に代入することで
dtdu=f(t)u2+g(t)u+h(t)
が得られる。
ここで z=x−u(t) とおく。このとき元の微分方程式は
dtdu+dtdz=f(t)(u2+2uz+z2)+g(t)(u+z)+h(t)
と書ける。これら2つの式の辺々の差を取ることで
dtdz=(2f(t)u(t)+g(t))z+f(t)z2
が得られる。これはベルヌーイの微分方程式(の s=2 の場合)であるため,一般解を求めることができる。
実際にさきほどの方法で解いてみる。w=z1−s,つまり w=z−1 とおくと,dtdw=−z21dtdz である。よって z に関する微分方程式は
−z2dtdwdtdw=(2f(t)u(t)+g(t))z+f(t)z2=−(2f(t)u(t)+g(t))w−f(t)
という w の線形微分方程式に帰着される。定数変化法により,定数 C を用いて
w=Cp(t)+q(t)
ただし
p(t)q(t)=exp(−∫2f(t)u(t)+g(t)dt)=−p(t)∫p(t)f(t)dt
である。w を x に戻すことで
x(t)=u(t)+w1=u(t)+Cp(t)+q(t)1
が得られる。
例:化学平衡
化学反応における濃度変化を解析するには微分方程式が有用です。リッカチの微分方程式が適用できる場合もあります。実際に例題を解いてみましょう。
例題:二酸化窒素の化学平衡
2NO2⇌N2O4
という化学反応を考える。二酸化窒素と四酸化二窒素の濃度について,x=[NO2],y=[N2O4] とおくとき,x,y は次の連立微分方程式を満たす。
⎩⎨⎧dtdx=−2(ax2−by)dtdy=ax2−by
なお a,b はそれぞれ化学反応の速度に関する定数である。また質量保存の法則より定数 c を用いて x+2y=c という関係式が成り立つ。
これらより x について
dtdx=−2ax2−bx+bc
という微分方程式が得られる。x の一般解を求めよ。
解
2次方程式
−2at2−bt+bc=0
の解は t=4a−b±b2+8abc である。これら2解をu,v (u>v) とする。今 x=u とすると,これは求めたい微分方程式の特殊解となる。
z=x−u とすると,z の満たす微分方程式は
dtdz=dtdx=−2a(u+z)2−b(u+z)+bc=−2az2−4auz−bz+(−2au2−bu+bc)=−2az2−Dz
となる。なお 4au+b=−b+b2+8abc+b=b2+8abc であり,簡単のため b2+8abc=Dとおいた。w=z−1 とおくことにより z の微分方程式を w の微分方程式に書きかえると,
−z2dtdwdtdw=−2az2−Dz=2a+Dz−1=2a+Dw
という微分方程式が得られる。これを解くと w=CeDt−D2a が得られる。
変数を戻すと,
x=z+u=w1+u=C−D2ae−Dte−Dt+u=C−D2ae−Dt(1−D2au)e−Dt+Cu
である。さらに
1−D2au=1−b2+8abc2a4a−b+b2+8abc=1−2b2+8abc−b+b2+8abc=−2b2+8abc−b−b2+8abc=−D2av
となるため,一般解は
x=C−D2ae−Dt(1−D2au)e−Dt+Cu=C−D2ae−Dt−D2ave−Dt+Cu=2aDC−e−Dt−ve−Dt+2aDCu=C′−e−DtC′u−ve−Dt
となる。なお C′ は定数である。
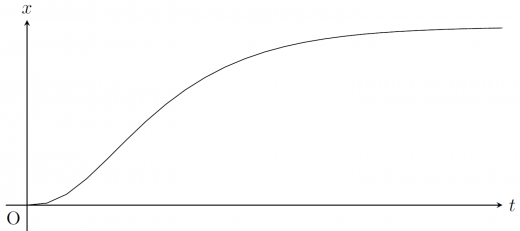
細かい計算が大変だったかもしれません。しかし,複雑な計算の結果,化学反応の過程における二酸化窒素の濃度を完全に求められました!
実際にグラフを描くと次のようになります。

(a=1,b=1,c=4,C′=25)
余談
リッカチの微分方程式は,リッカチ方程式やリッカチ形と表記されることもあります。本によっては「リッカティ」などの表記をする場合もあります。しかし,リカッチの微分方程式では決してありません! 綴りはRiccatiです!
身近な現象を微分方程式で表現し,実際に計算してみると楽しいです。