水平線,地平線までの距離の計算方法と例
更新
水平線までの距離はだいたい4km〜5km
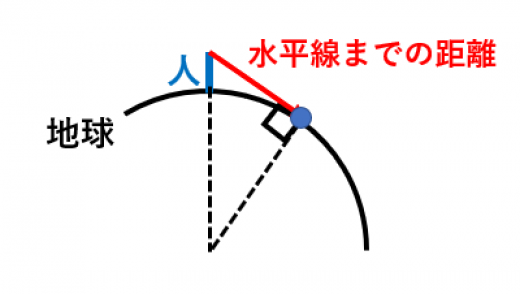
水平線(地平線も同じ)までの距離を計算する方法を解説します。
水平線までの距離
水平線までの距離
水平線までの距離はおよそ です。この式は後で導出します。ただし,
- は地球の半径で, kmです。
- は水平線を見る人の身長(正確には目の高さ)です。
例えば km (170cm)として計算すると,有効数字3桁で 水平線までの距離は kmとなります!
水平線・地平線までの距離が4~5kmくらいというのは直感に合うのではないでしょうか?
水平線・地平線までのいろいろな距離
水平線・地平線までのいろいろな距離
水平線までの距離公式 を使っていろいろな距離を計算してみました。
- 子供(身長1m)から見た水平線までの距離: km
- 高身長の人(身長2m)から見た水平線までの距離: km
- スカイツリーの展望台(高さ450m)から見た地平線までの距離: km
- 富士山(高さ3.78km)から見た地平線までの距離: km
富士山とスカイツリーの距離は kmくらいなので片方からもう片方が(目が十分良い人なら)観測できます。 - 飛行機(高さ10km)から見た地平線までの距離: km
羽田空港上空10000mからは名古屋くらいまで見えるということです。
計算式の導出
計算式の導出
「水平線までの距離」を2通りの解釈で考えて計算してみます。いずれも上記公式を導出できます。
(目と)水平線までの距離 は図の赤い線分 の長さ。三角形 に三平方の定理を使う。
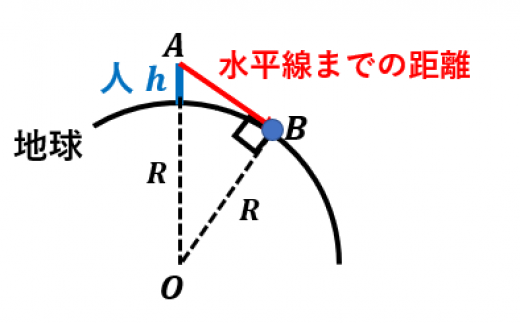 , なので,
, なので,
よって
また,身長 は地球の半径 より十分小さいので を無視すると,
(足元と)水平線までの地面をたどった距離 は図の緑の弧の長さ。
 中心角を
とおくと,
中心角を
とおくと,
一方, より (注1)
以上二つの式より,
ここからは近似解を求める。 であり, なので と近似できる(注2)。
つまり,さきほどの式は ,つまり となる。さらに, と近似すると,
-
注1: は の逆関数です。→逆三角関数(Arcsin,Arccos,Arctan)の意味と性質
-
注2:コサインの二次近似です。→三角関数の不定形極限
北海道の大自然を見ていたときに思いついた記事です。
Tag:難しめの数学雑学・ネタまとめ











