伸開線(インボリュート)と縮閉線(エボリュート)の意味と計算例
伸開線(インボリュート)と縮閉線(エボリュート)の意味と計算例を紹介します。曲線に関するいろいろな計算(媒介変数表示・接線・法線・曲率)の練習になる楽しい話題です。
伸開線(インボリュート)の意味と例
伸開線(インボリュート)の意味と例
曲線に対して,その曲線に巻きつけられた糸をたるませないようにほどいていくときに糸の端点が描く軌跡のことを伸開線(Involute)と言う。
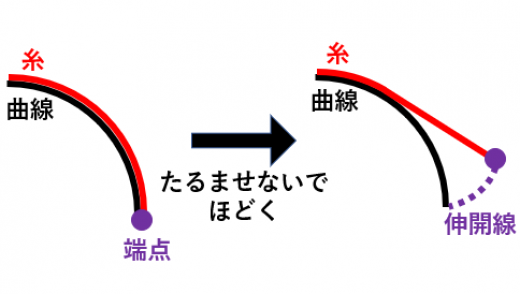
円 の伸開線(の媒介変数表示)を求めよ。ただし,糸の端点を とし,反時計回りにほどいていく。
までほどけたとき,糸の端点の位置を求める。
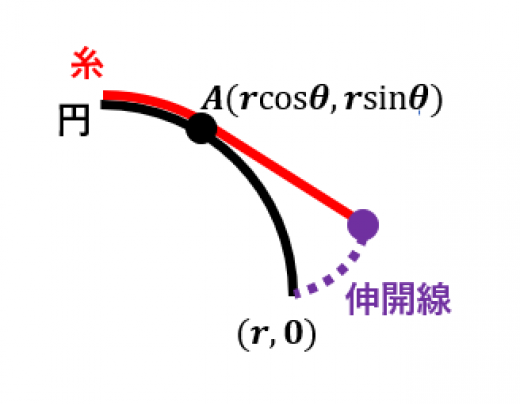
- ほどけた糸の長さは からの円弧の長さなので
- における単位接線ベクトルは
よって,糸の端点の位置は,
これはインボリュートと呼ばれる曲線の媒介変数表示です(伸開線のことを広くインボリュートと呼ぶこともあり,円の伸開線のことをインボリュートと呼ぶこともあるようです)。
縮閉線(エボリュート)の意味
縮閉線(エボリュート)の意味
曲線に対して,曲率円の中心の軌跡を縮閉線(Evolute)と言う。
曲率円とは,その付近で曲線を円とみなしたときの円のことです。詳細は,曲率・曲率半径の感覚的な意味と求め方で解説しています。
以下では,縮閉線を求める2つの計算例を紹介します。例2は難しいですが結果が楽しいです。例3は誘導付きで入試で出そうです。
縮閉線の求め方と例(媒介変数表示の場合)
縮閉線の求め方と例(媒介変数表示の場合)
例1で求めたインボリュート,つまり
()で表される曲線の縮閉線を求めよ。
方針:
-
における曲率半径を とします。 は曲率・曲率半径の感覚的な意味と求め方に記載の公式で計算できます。
-
曲率円の中心に向かう単位ベクトル(左向きの単位法線ベクトル)は
-
曲率円の中心は,
まず,1階微分と2階微分を計算しておく。
-
曲率半径の公式より,
-
法線ベクトルは
-
曲率円の中心は,
これは,中心が原点で半径が の円である。
伸開線と縮閉線の関係
伸開線と縮閉線の関係
例1・例2で見たように,円の伸開線はインボリュートで,インボリュートの縮閉線は円でした。より一般に以下が成立します。
伸開線の縮閉線は元の曲線になる。
-
伸開線はスタート位置(糸の長さ)によって変わるので,曲線 の伸開線は無数にあります。ですが,どの伸開線を選んでもその縮閉線は に戻ります。
-
たしかに,「糸の端点」の「曲率中心」はもとの点になりそうですね。

縮閉線の求め方と例(y=f(x) 型の場合)
縮閉線の求め方と例(y=f(x) 型の場合)
放物線 の縮閉線(の媒介変数表示)を求めよ。
媒介変数表示の場合と同様,曲率半径 と単位法線ベクトル を計算するだけです。
上の点 において,
-
曲率半径は
-
接線の傾きが なので法線の傾きは である。よって曲率円の中心に向かう単位法線ベクトルは,
よって,
よって,曲率円の中心は,
ちなみに,サイクロイドの縮閉線はサイクロイドになります。
「伸」の反対は「縮」で「開」の反対は「閉」なので,伸開線の縮閉線は元の曲線であってほしいですね。











