証明
A(cosθ,sinθ),B(cos(θ+h),sin(θ+h)) とおく。
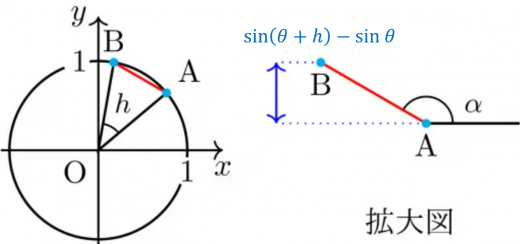
上図から
hsin(θ+h)−sinθ=hABsinα
を得る。
三角形 OAB に余弦定理を用いることで
AB2AB=OA2+OB2−2OA⋅OB⋅cos∠AOB=1+1−2cosh=2(1−cosh)=2(1−cosh)
を得る。こうして AB が h によって表された。
また,h が 0 に近いとき,AB は A における単位円の接線に近づくので,h→0limα=θ+2π を得る。
よって,
h→0limhsin(θ+h)−sinθ=h→0limhABsinα=h→0limh2(1−cosh)sinα=h→0limh22(1−cosh)sinα=sin(θ+2π)=cosθ
を得る。













