増減表の書き方
増減表とは,それぞれの区間で 関数 が増加するか減少するかなどを表した表のことです。

増減表の意味や書き方を詳しく解説します。
関数の増減
関数の増減
まずは,増減表を書くための前提知識です。
- なら関数は増加(グラフは右上がり)
- なら関数は減少(グラフは右下がり)
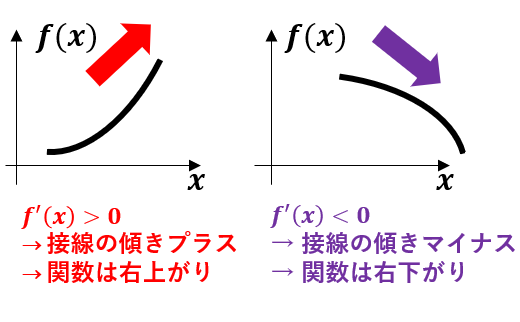
つまり,微分 がプラスなのかマイナスなのかを調べることで,グラフが右上に進むか右下に進むかがわかります。
増減表の例
増減表の例
例えば の増減表は図のようになります(増減表の書き方は後で詳しく説明します)。

(①~⑤は説明のために書いていますが,答案では不要です)
増減表から以下の①~⑤が読み取れるので, のグラフの概形がかけます。
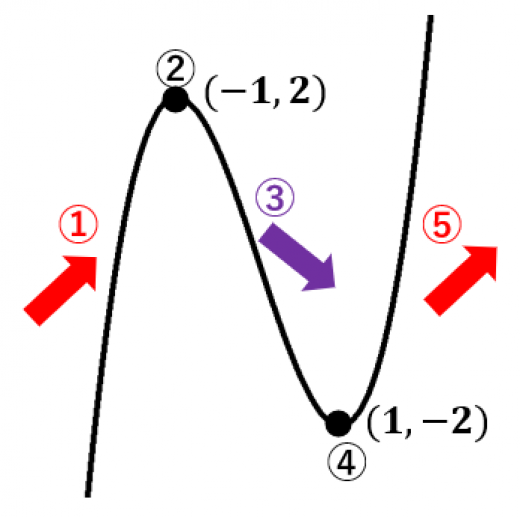 ①右上に進んで
② を通り
③右下に進んで
④ を通り
⑤右上に進む
①右上に進んで
② を通り
③右下に進んで
④ を通り
⑤右上に進む
つまり,増減表はグラフを書くための情報を集めた表と言えます。
増減表の書き方
増減表の書き方
具体的に の増減表の書き方を説明します。増減表は の符号を調べることで書けます。
の増減を調べよ。
ステップ1: の符号を調べる
微分すると,
符号を調べるために を解く。つまり,
よって, の解は
そして,
- , のとき
- のとき
ステップ2: 増減表を書く
ステップ1の結果をもとに,増減表を書いていく。
- 1行目は とその間の区間のマスを書く
- 2行目は各区間における の符号()を書く
- 3行目は2行目の情報をもとに の情報を書く( が なら右上, なら右下, なら具体的な値を書く)

で極大値 , で極小値 を取ることが分かる。
このように,関数の増減だけを調べればよい場合,一階微分まで計算して ,, の3行の増減表を書きます。
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題56も参照してください。
凹凸や変曲点も調べる場合(数III)
凹凸や変曲点も調べる場合(数III)
さきほどのステップ2の結果からグラフの概形を描くことも可能ですが,さらに二階微分も計算して ,,, の4行の増減表を書いてみます。
の増減,凹凸,変曲点を調べ,グラフの概形を描け。
ステップ2(改): の符号を調べる。
であったので,
よって, の解は
また,
のとき
のとき
ステップ3: 増減表を書く。
まずはステップ1の情報をもとに の情報を書く(1行目と2行目)。

次にステップ2(改)の情報をもとに の情報を書く(3行目)。
最後に2行目と3行目の符号をもとに4行目を書く。
ステップ4: グラフを描く。

ステップ3で得た増減表の の行を参考にすると,グラフの概形は図のようになる。
のとき上に凸, のとき下に凸,変曲点は であることが分かる。
増減表の書き方補足
基本は3行の場合と同じですが,4行目の矢印は4種類あります。
がマイナスのところでは接線の傾きは減少していくので,時計回りの矢印を書きましょう。
逆に, がプラスのところでは接線の傾きは増加していくので,反時計回りの矢印を書きましょう。
解答が長い場合,複数のステップに分解して自分の理解が浅い部分を特定しましょう。











