三角関数sec, cosec, cotと記号の意味

• $\dfrac{1}{\sin x}$ や $\dfrac{1}{\cos x}$ はいろいろなところに登場するので，「それ自体に簡単な記号を定めよう」という記号です。一部の教科書では実際に使われています。
• $\sec$ のことを正割（セカント），$\csc$ のことを余割（コセカント），$\cot$ のことを余接（コタンジェント）と呼びます。
• 例えば $1+\tan^2 x=\sec^2 x$ などのように使われます。分数の表記を避ける事ができます。
• しかし，「$\dfrac{1}{\sin x}$ と書くより $\mathrm{cosec}$ と書いたほうが楽だ」と思う人はほとんどいないと思います。分数を避けるのか $\sec$ などの新しい記号を避けるのか？　個人的には分数を避けるメリットよりも記号が増える煩わしさの方が重いので $\sec,\mathrm{cosec},\cot$ は使わないという立場です。
• しかし，一部ではまだ使われているため，自分が使わないとしても，記号が出てきたときに理解できる必要はあります。

セカントの図形的意味

セカントは英語で secant と書きます。これは割線という意味です。

割線とは，ある曲線に2点以上で交わる直線のことです。

次の図を見てください。

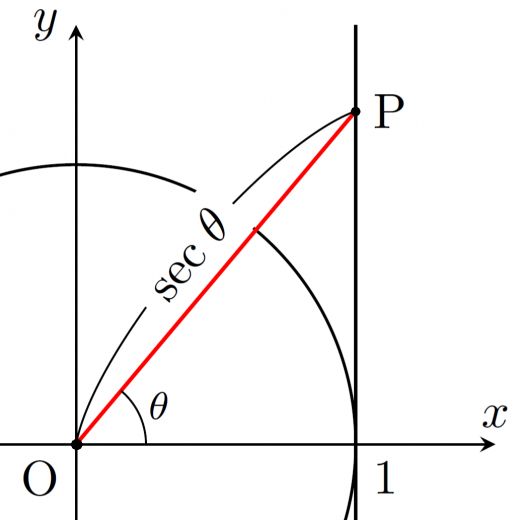
単位円に対して「原点を通り傾き $\theta$ の直線」は割線です。さらに，$(1,0)$ における接線との交点を $\mathrm{P}$ としたとき，$\sec \theta = \mathrm{OP}$ となります。

このように $\sec$ は，円の割線にまつわる長さを表しています（少し無理があるような気がしますが）。

逆三角関数

• $\sin x$ の逆関数を $\sin^{-1}x$ と表記してもよいのですが，$\mathrm{Arcsin}x$ と表記することが多いです（→逆三角関数(Arcsin,Arccos,Arctan)の意味と性質）。$\sin^{-1}x$ は $\dfrac{1}{\sin x}$ と勘違いするおそれがあるからです。

• 私は新しい記号が増える煩わしさより，意味を間違えられる危険性が勝つので $\mathrm{Arcsin}$ を使います（個人的な見解です，$\sin^{-1}x$ を使う人もいます）。

指数関数

• 高校数学ではあまりみかけませんが，指数関数 $e^x$ を $\exp(x)$ と表記することがあります。
• これは記号も増えて表記も長くなってデメリットしかないように思えますが，$e^{\frac{x^2+1}{2}}$ のように指数に乗る式が複雑になったときに威力を発揮します。 $\exp(\tfrac{x^2+1}{2})$ の方が見やすいですし，式が上下に広がるのを防いでくれます。

$\sec , \csc$ はあまり登場しませんが，$\cot$ は無限級数の文脈でしばしば登場します。

級数展開

$\cot x$ は $0$ 近傍で $$\cot x = \sum_{n=0}^{\infty} \dfrac{(-1)^{n} 2^{2n} B_{2n}}{(2n)!}x^{2n-1} \quad (0 < |x| < \pi)$$ と級数展開（ローラン展開）されます。 →ローラン展開の意味・計算方法・特異点の分類

これは $\tan$ のマクローリン展開 → tanxの高階微分とマクローリン展開 $$\tan x= \sum_{n=1}^{\infty}\dfrac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}}{(2n)!}x^{2n-1}$$ から計算できます。

部分分数分解

また，（複素関数の範囲で）部分分数分解した $$\pi \cot \pi z= \dfrac{1}{z} + \sum_{n=1}^{\infty} \dfrac{2n}{z^2 - n^2}$$ という表現もあります。

複素解析の道具を使うことで証明できます。