逆関数の微分公式を例題と図で理解する

(1) もとの関数 $y=x^2+1$ を微分すると $y'=2x$ である。これに $x=1$ を代入すると微分係数は $2$

(2) $y=x^2+1$ を $x\geqq 0$ の範囲で $x$ について解くと，$x=\sqrt{y-1}$
よって，逆関数は $y=\sqrt{x-1}$

(3) この逆関数を微分すると，$\dfrac{1}{2\sqrt{x-1}}$ である。これに $x=2$ を代入すると微分係数は $\dfrac{1}{2}$

$y=f(x)$ の逆関数を $g$ とおくと，逆関数の定義より $x=g(y)$

これを合成関数の微分公式で両辺を $x$ で微分すると，

$1=\dfrac{dy}{dx}\dfrac{dg(y)}{dy}$

よって，両辺を $\dfrac{dy}{dx}$ で割ると

$\dfrac{dg}{dy}=\dfrac{1}{\frac{dy}{dx}}$ を得る。

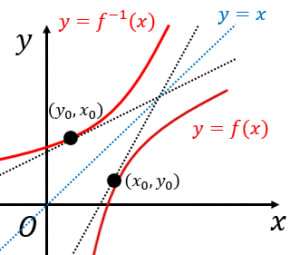
図で，以下の2つの直線（黒い点線）を見てみよう：

1. $y=f^{-1}(x)$ の $(y_0,x_0)$ における接線
2. $y=f(x)$ の $(x_0,y_0)$ における接線

この2本の傾きは「逆数」の関係がある。なぜなら，

• 2本の接線は $y=x$ に関して対称（→逆関数の３つの定義と使い分け）
• $y=x$ に関して対称な2本の接線の傾きが互いに逆数の関係にあることは簡単に分かる。

つまり1（逆関数の微分）と2（もとの関数の微分）は互いに逆数の関係にある。

$y=\log x$ の微分を求めたい。これを変形する（$x$ について解く）と，

$x=e^y$

この両辺を $y$ で微分すると，

$\dfrac{dx}{dy}=e^y$

よって，逆関数の微分公式より，

$\dfrac{dy}{dx}=\dfrac{1}{\frac{dx}{dy}}=\dfrac{1}{e^y}$

となる。

最後に $e^y=x$ を使うと，結局

$\dfrac{dy}{dx}=\dfrac{1}{x}$ となる。

$y=\log x$ の導関数を求めたい。

つまり，$y=\log x$ の $(x_0,y_0)$ における接線の傾き (*) を求めればよい。

これは「図による理解」で述べたことにより

$y=e^x$ の $(y_0,x_0)$ における接線の傾き (**) の逆数に等しい。

$y=e^x$ の微分は $y'=e^x$ なので，

(**) は $e^{y_0}$ である。

よって，(*) は，$\dfrac{1}{e^{y_0}}$ となる。

また，$(x_0,y_0)$ は $y=\log x$ 上の点なので，$y_0=\log x_0$ である。

結局，(*) は $\dfrac{1}{x_0}$ となる。

この議論は定義域内の全ての $x_0$ で成り立つので，$y=\log x$ の導関数は $y=\dfrac{1}{x}$ である。