1/3公式と1/12公式の意味と証明【二次関数・三次関数と面積】
- 1/3公式と1/12公式(二次関数版)と1/12公式(三次関数版)いう3つの公式を紹介します。
- 二次関数(放物線)や三次関数に関する面積をすばやく計算できる公式です。
1/3公式とその証明
1/3公式とその証明
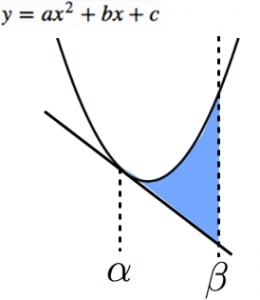
- 放物線
- 放物線と で接する接線
という3つのグラフで囲まれた部分の面積は,
の場合について証明する(他の場合も全く同様)。
愚直に計算するのではなく,「接線」であることを利用して被積分関数を因数分解する:
よって,求める面積は
1/12公式(二次関数版)とその証明
1/12公式(二次関数版)とその証明
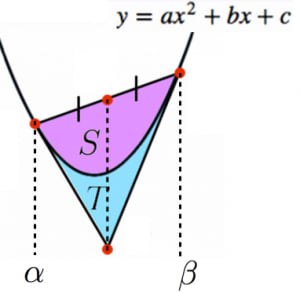
放物線 の2本の接線の接点の 座標を とおくとき,放物線と2本の接線で囲まれた部分の面積 は,
1/12公式の証明を2通り紹介します。まずは,2分割して1/3公式を使う方法です。
次は,有名な1/6公式(後述)を使った1/12公式の証明です。
1/12公式(三次関数版)とその証明
1/12公式(三次関数版)とその証明
二次関数版の1/12公式とは別に,三次関数に関する1/12公式もあります。どちらも1/12公式と呼ばれるので紛らわしいです。
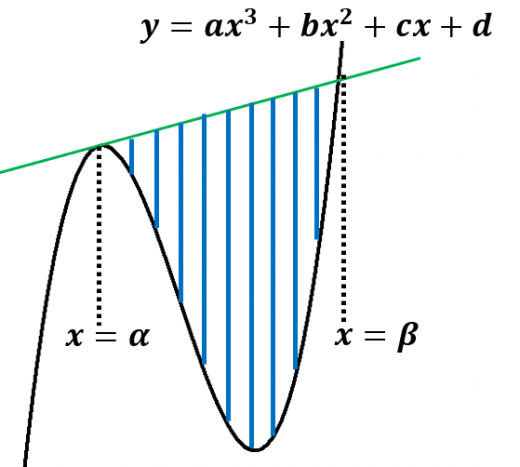
- 三次関数
- 三次関数と で接し, でも交わる直線
で囲まれた部分の面積は,
, の場合について証明する(他の場合も全く同様。
よって,求める面積は
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題220では,1/12公式を使う例題と3通りの解法を紹介しています。
1/6公式
1/6公式
1/3公式・1/12公式と似ている有名な公式に1/6公式があります。
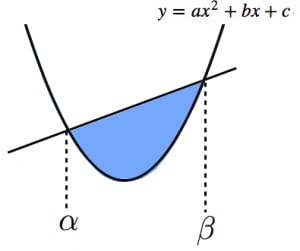
放物線 と直線 の交点の 座標を とおくとき,
放物線と直線で囲まれた部分の面積は,
証明は1/6公式とその証明を参照してください。
4つの公式の共通点
4つの公式の共通点
1/3公式・1/12公式・1/6公式は似ています!
- や直線の式に直接依存せず と のみで面積が決まります。
- 全て,(ただし は区間幅)という形をしています。1/3公式では ,1/12公式では ,1/6公式では です。二次関数についての公式では ,三次関数についての公式では です。
- 証明のポイントは,「展開しない」です。因数分解された式の積分をわざわざ展開してから行うのではなく,うまく処理すれば計算が楽になります。これは非常に重要な考え方で,三次関数が関係してくる場合もしばしば使えます。
- 公式の丸暗記でかなりの時間短縮&検算に役立ちます。
1/6公式と1/3公式は覚えておくべきです。1/12公式もたまに役立つので余力がある人は覚えておきましょう。










