ジョルダンの不等式とその３通りの証明

• 数3の微分で登場する非常に有名な不等式です。

• 特に，右側はマクローリン型不等式（三角関数）でも紹介した特に有名な不等式です。

• ジョルダンの不等式は $\sin x$ を上と下から一次関数でおさえる不等式です。

• 不等式の証明としてそのまま出題されることもありますし，難関大学では「ジョルダンの不等式を用いて $\sin x$ を評価→はさみうちの原理を用いて何かしらの極限を求める」という流れの問題も出題されます。

• 例えば右側の不等式は $\displaystyle\lim_{x\to 0}\dfrac{\sin x}{x}=1$ を示すために使います。sinx/xについて覚えておくべき2つのこと

以下ではジョルダンの不等式の3通りの証明を紹介します。

1. 微分を用いる証明
2. グラフを用いる証明
3. 図形的な証明

両辺の差を取って微分し非負であることを示すという自然な方法です。

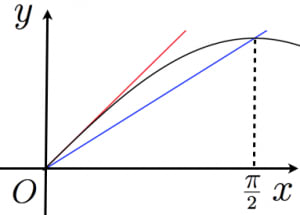
$y=\dfrac{2}{\pi}x,\sin x,x$ のグラフをそれぞれ書いてみればジョルダンの不等式が理解しやすいです。 特に左側の不等式が成立することは明らかです。

「ジョルダンの不等式を証明せよ」という直接的な問題に対しては方法1が無難ですが，ジョルダンの不等式を応用して極限の値を求める応用問題などの場合はこちらの方法で十分です。

図において「赤の長さ $\leq$ 紫の長さ $\leq$ 青の長さ」が成立することから証明されます。

$O$ を中心とした半径1の円を考えます。

• 赤は線分 $AB$ の長さ：$\sin x$
• 青は $AB$ を半径として $B$ を中心とする円の弧 $AD$ の長さ：$\sin x\cdot\dfrac{\pi}{2}$

よって $\sin x \leq x \leq \dfrac{\pi}{2}\sin x$ となり，これはジョルダンの不等式と同値です。

※厳密には $D$ が円の外側にあることを示す必要がありますが，これは三角不等式 $OA <OB+AB$ より $OC <OD$ となり成り立ちます。