サイクロイド曲線のグラフと面積・体積・長さ
更新
この記事では,サイクロイドに関する面積,体積,長さの求め方を解説します。
サイクロイド曲線 ()について,
- と 軸で囲まれた部分の面積は
- 軸周りの回転体の体積は
- 長さは
積分計算のよい練習になります。
準備:サイクロイドのグラフ
準備:サイクロイドのグラフ
サイクロイドは「円を転がした時の円周上の1点が動く軌跡」であり,媒介変数表示を用いて表される代表的な曲線です。
面積や体積,長さを求める準備として,まずはサイクロイドのグラフを描いてみます。
サイクロイドの媒介変数表示 に対して, を で微分すると, となります。 の範囲では は正なので, が増加するにつれて は増加します。
また, を で微分すると, となるので が増加するにつれ, の範囲では は増加, の範囲では は減少します。
また, の符号について考えると, より, が成立します。
これらに基づくと,グラフの概形は図のようになります。軌跡を描く点は右に動きつつ, までは上へ,それ以降は下へ動きます。
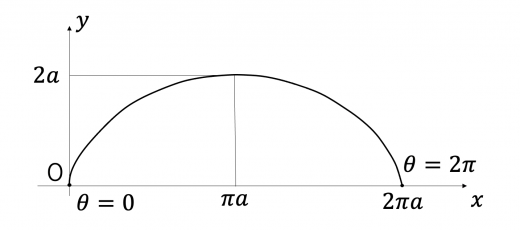
サイクロイドの面積を積分で求める
サイクロイドの面積を積分で求める
サイクロイド曲線と 軸で囲まれた部分の面積 は,公式より, で計算できます。これを,置換積分を用いて で積分していきます。 であり, が となるとき, は となります。よって, ここで, により
これより, は転がる円の面積のちょうど 倍であることがわかります。
やっていることは単純で,ただ置換積分をしているだけです。置換積分は計算ミスをしやすいので,落ち着いて計算しましょう。
最短で得点力を上げる!高校数学の問題集〈典型250問〉 の問題236では,ガウスグリーンの公式を用いた別解も紹介しています。
サイクロイドの回転体の体積を積分で求める
サイクロイドの回転体の体積を積分で求める
回転体の体積を求める公式: を使うと, 軸周りの回転体の体積 は ここで, により となります。
公式に当てはめてしまえば,あとは単純な計算問題でした(計算量は重いですが)。
サイクロイドの長さを積分で求める
サイクロイドの長さを積分で求める
曲線の長さを求める公式: を使うと,サイクロイド曲線の長さ は ここで, を用いると, より であるから,
よって絶対値がそのまま外せて となります。
サイクロイドの曲線の長さには が出てきません。半径の 倍という綺麗な結果になります。
が積分に出てきて少し戸惑うかもしれませんが,半角の公式を使うことでルートを外せることを知っておきましょう。また,ルートを外す際には絶対値記号をつけることを忘れずに。
サイクロイドは試験でよく題材として取り上げられるので,結果を覚えておくと検算等に使えるかもしれません。









