三重対角行列の特殊形の固有値は綺麗
更新
のように,
対角成分とそれに隣接する成分(副対角成分)以外が であるような正方行列を三重対角行列と言う。
三重対角行列について
三重対角行列について
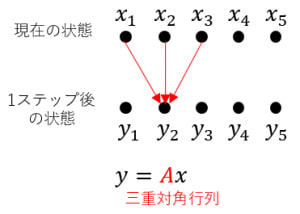
やや抽象的ですが「自分と自分の両隣の現在の値の重みつき和」が1ステップ先の状態となるような系を,行列を用いて表現すると,三重対角行列が登場します。
なんとなく応用数学や物理で登場しそうな気がしますね。
三重対角行列は一般の行列よりも扱いやすいです。例えば,漸化式を用いることで行列式が で計算できます。Tridiagonal matrix (Wikipedia)
特殊形の固有値(前半)
特殊形の固有値(前半)
三重対角行列の中でも対角成分が全て ,副対角成分が全て であるようなものを と書くことにします。
この記事の残りでは の固有値,固有ベクトルについて考えます(美しいですよ!)。 →固有値,固有ベクトルの定義と具体的な計算方法
が の固有値 に対する固有ベクトルとする。
このとき, は の固有値 に対する固有ベクトルとなる。
つまり, の固有値と固有ベクトルが分かれば の固有値と固有ベクトルも分かるというわけです。
同じサイズの単位行列を とすると,
となる。
よって, のとき,
となる。
特殊形の固有値(後半)
特殊形の固有値(後半)
というわけで,サイズ の の固有値と固有ベクトルについて考えてみましょう。
とおくと,
に対して, は の固有値 に対する固有ベクトルとなる。
固有値は単位円の上半分を 等分して 座標を見る(そして2倍する)というイメージです。三角関数が登場するのが面白いです。
を証明すればよい。
つまり,
を確認すればよい。
1つめは から分かる。2つめと3つめは三角関数の和積公式から分かる( より,3つめは2つめの特殊ケースとみなせる)。
なお, の長さは になります。位相が等差数列である三角関数の和の公式を使って計算できます。
ちなみに のように左上右下ラインが同じ成分であるような行列を,テプリッツ行列と言います。記事の後半で扱った行列は「対称三重対角テプリッツ行列」です。











