二次曲線（楕円，放物線，双曲線）の極座標表示

極方程式 $r=\dfrac{l}{1+\varepsilon\cos\theta}$ で表される曲線がどのような形状をしているのかを分析するために，直交座標に変換します。

途中で両辺二乗するために前処理が必要になります。

どのような二次曲線になるかは離心率 $\varepsilon$ によります。以下ではそれぞれについて見てみます。

離心率が $0$ のとき，極方程式は $r=l$ ，つまり原点を中心とする半径 $l$ の円を表します。これは自明でつまらない例ですね。

(*)を変形していく：

$(1-\varepsilon ^2)x^2+2l\varepsilon x+y^2=l^2$

$(1-\varepsilon^2)\left(x+\dfrac{l\varepsilon}{1-\varepsilon^2}\right)^2+y^2=\dfrac{l^2}{1-\varepsilon^2}$

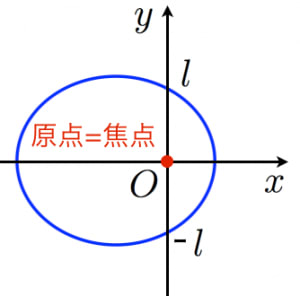
これは $1-\varepsilon^2 > 0$ のとき，楕円を表す。

（ただし中心は原点でない。実は楕円の焦点の一つが原点となる）

離心率が $1$ のとき，(*)において $x^2$ の項は消える：

$y^2=l^2-2lx$

$y^2=-2l \left( x-\dfrac{l}{2} \right)$

これは，放物線 $y^2=-2lx$ を $x$ 軸方向に $\dfrac{l}{2}$ 平行移動したもの。楕円の場合と同じく放物線の焦点は原点。

離心率が $1$ より大きいとき，楕円のところで導出した式の両辺を $-1$ 倍する：

$(\varepsilon^2-1)\left(x+\dfrac{l\varepsilon}{1-\varepsilon^2}\right)^2-y^2=\dfrac{l^2}{\varepsilon^2-1}$

これは双曲線を平行移動したものである。同じく焦点の一つが原点。

Tag:数学Cの教科書に載っている公式の解説一覧