楕円積分の意味と身近な4つの例
更新
楕円積分の意味と,楕円積分が現れる4つの例を紹介します。
-
のことを第二種楕円積分という。 -
のことを第一種楕円積分という。
- と はパラメータです。
- ただの定積分に見えますが,一般に,楕円積分は解析的に計算できません(原始関数が簡単な形で書けません)。
第二種楕円積分が活躍する例
第二種楕円積分が活躍する例
楕円の周の長さ
曲線の長さを計算する積分公式(弧長積分)を使って楕円の周の長さを計算してみます。
楕円の周の長さは,第二種楕円積分で表される。
楕円 の周の長さを計算する。 と媒介変数表示すると, の部分の長さは,
特に,楕円全体の長さは
- は楕円の離心率です。→離心率の意味と関連する計算
- 楕円全体の長さに出てきましたが の場合の第二種楕円積分を第二種完全楕円積分と言います。
- もっと頑張って級数展開することもできます。→楕円の周の長さの求め方と近似公式
正弦曲線の長さ
正弦曲線の長さは,第二種楕円積分で表される。
の から までの長さは,
第一種楕円積分が活躍する例
第一種楕円積分が活躍する例
単振り子の周期
単振り子の周期は,第一種楕円積分で表される。
このように, の場合の第一種楕円積分を第一種完全楕円積分と言います。
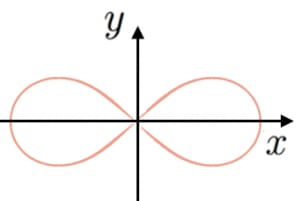
レムニスケートの長さ
レムニスケート曲線: の長さは,第一種楕円積分で表される。
ヤコビの標準形
ヤコビの標準形
ルジャンドルの標準形において と置換すると,定積分を の簡単な式(ルート+有理式)に変形できます。
-
のことを第二種楕円積分という。 -
のことを第一種楕円積分という。
- 第二種楕円積分(ルジャンドルの標準形) において, と置換すると, より, あらためて と置けばよい。
- 第一種楕円積分も同様
特殊ケース
特殊ケース
楕円積分は, または の場合は計算できます。
-
の場合,ルジャンドルの標準形で考えると, つまり,ヤコビの標準形で考えると, となる。
-
の場合の第二種楕円積分は,ルジャンドルの標準形で考えると, つまり,ヤコビの標準形で考えると, となる。
-
の場合の第一種楕円積分は,ヤコビの標準形で考えると, となる。
なお,ヤコビの標準形で考えたときの,楕円積分の逆関数をヤコビの楕円関数と言います。上の例からわかるように, や はヤコビの楕円関数の特殊ケースです。
より一般に ( は定数, は3次か4次の多項式, は有理式)という形の積分のことを楕円積分と言います。この記事では,その中で重要な2種類の楕円積分を紹介しました。











