楕円

更新 2025/05/24

楕円とは

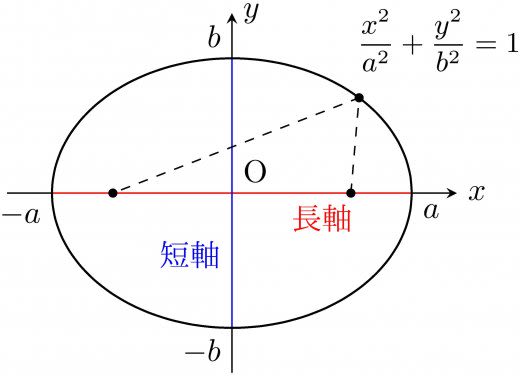
2点からの距離の和が一定である点の軌跡を楕円と言う。また，この2点のことを焦点という。

楕円の端を結ぶ直線のうち，長いものを長軸，短いものを短軸という。

この記事では楕円の定義とその基本的な性質を紹介します。

双曲線とは似た性質が多いので，こちらもどうぞ。→ 双曲線

楕円の基礎知識

焦点がx軸上にある楕円

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ は楕円を表す。この楕円は，

$a > b$
$(\pm a, 0 )$ ， $(0,\pm b)$ を通る。
二点 $(\pm\sqrt{a^2-b^2},0)$ からの距離の和が $2a$ で一定である。

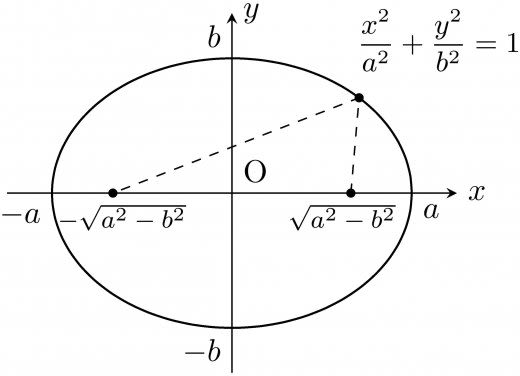
焦点がx軸上にある楕円

証明

$(\pm c , 0)$ からの距離の和が $2a$ のとき， $\sqrt{(x+c)^2+y^2} + \sqrt{(x-c)^2 + y^2} = 2a$

$\sqrt{(x+c)^2+y^2} = 2a - \sqrt{(x-c)^2 + y^2}$

両辺を2乗して整理すると， $4cx - 4a^2 = - 4a \sqrt{(x-c)^2 + y^2}$ である。辺々を $4$ で割って2乗すると $c^2x^2 - 2a^2cx + a^4 = a^2 \{ (x-c)^2 + y^2 \}$ である。整理すると $(a^2-c^2) x^2 + a^2 y^2 = a^2 (a^2-c^2)$ となる。ここで $b = \sqrt{a^2 - c^2}$ とおくと $b^2 x^2 + a^2 y^2 = a^2 b^2$ 辺々を $a^2b^2$ で割って $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ を得る。さらにこのとき $c =\pm \sqrt{a^2 -b^2}$ となる。

練習問題1

楕円 $\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$ の焦点を求めよ。

練習問題1の解答

解答

さきほどより焦点は $(\pm\sqrt{9-4},0)$ となる。つまり $(\sqrt{5},0)$ と $(-\sqrt{5},0)$ である。

焦点がy軸上にある楕円

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ は楕円を表す。この楕円は，

$a < b$
二点 $(0,\pm\sqrt{b^2-a^2})$ からの距離の差が $2b$ で一定である。
$(\pm a, 0 )$ ， $(0,\pm b)$ を通る。

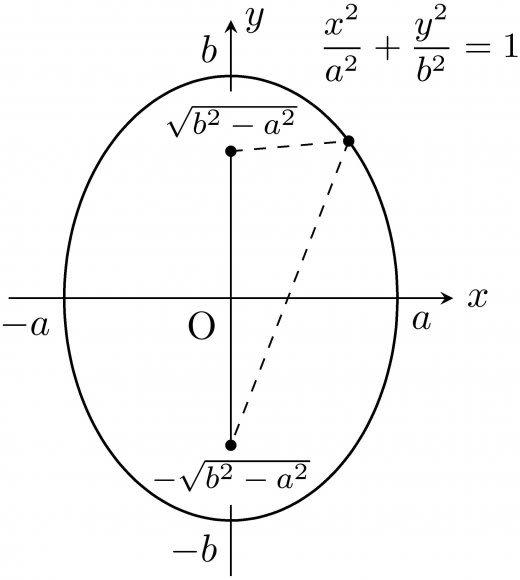
焦点がy軸上にある楕円

証明は焦点が $x$ 軸上にあるときと同様です。

入試でよく出る性質

入試で頻出の性質を紹介します。

面積

定理

楕円 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ の面積は $\pi ab$ である。

証明は楕円の面積公式の３通りの導出をご覧ください。

平行移動

ここまでは，原点中心の楕円でしたが，そうでない場合もあります。グラフの平行移動（具体例と公式の証明）を使って考えます。

練習問題2

$\dfrac{(x-2)^2}{5} + (y-3)^2 = 1$ の焦点を求めよ。

練習問題2の解答

解答

$\dfrac{x^2}{5}+y^2 = 1$ という「原点中心の楕円」を $x$ 軸方向に $2$ ， $y$ 軸方向に $3$ 平行移動したものである。

原点中心の楕円の焦点は，前の公式より $(\pm \sqrt{5-1} , 0)$ ，つまり $(\pm 4,0)$ である。

求める焦点は $(\pm 4,0)$ を $x$ 軸方向に $2$ ， $y$ 軸方向に $3$ 平行移動したものである。よって $(2,7), (2,-1)$ である。

接線

楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 上の点 $(x_0,y_0)$ における接線の方程式は， $\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$ である。

接線の方程式の導出は，楕円の接線を求める公式とその証明を参照ください。

練習問題3

$\dfrac{x^2}{15} + \dfrac{y^2}{10} = 1$ の $(3,2)$ における接線を求めよ。
$\dfrac{(x-2)^2}{15} + \dfrac{(y+3)^2}{10} = 1$ の $(5,-1)$ における接線を求めよ。

練習問題3の解答

解答

公式から $\dfrac{x}{5} + \dfrac{y}{5} = 1$ である。
問題の楕円は $\dfrac{x^2}{15} + \dfrac{y^2}{10} = 1$ を $x$ 軸方向に $2$ ， $y$ 軸方向に $-3$ 平行移動したものである。 $(5,-1)$ は $(3,2)$ に対応するため， $\dfrac{x}{5} + \dfrac{y}{5} = 1$ を $x$ 軸方向に $2$ ， $y$ 軸方向に $-3$ 平行移動した直線を考えればよい。よって $\dfrac{x}{5} + \dfrac{y}{5} = \dfrac{4}{5}$ である。

媒介変数表示

楕円 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}=1$ は $\begin{cases} x = a \cos \theta\\ y = b \sin \theta \end{cases}$ と媒介変数表示できます。

詳細は，→楕円・双曲線の媒介変数表示の3通りの方法

その他基礎知識

入試で登場することは少ないですが，重要な基礎知識を紹介します。
準線と離心率楕円は「2点からの距離の和が一定」で定義されましたが，「点 F\mathrm{F}F からの距離と直線 lll からの距離の比が一定」で定義することもできます。
この直線 lll を準線と言い，比を離心率と言います。楕円の離心率は 111 より小さいです。
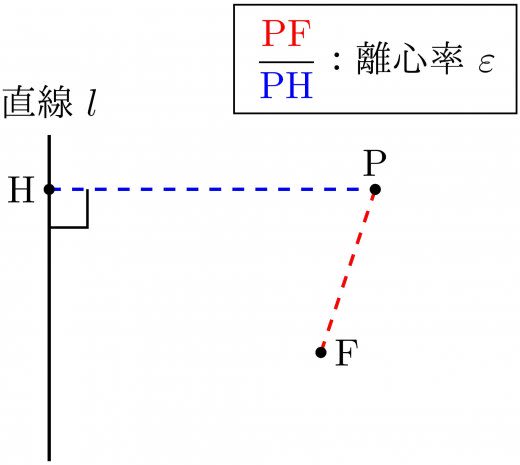
楕円 x2a2+y2b2=1 (a>b)\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \ (a > b)a2x2​+b2y2​=1 (a>b) について，準線（の1つ）は x=a2a2−b2x=\dfrac{a^2}{\sqrt{a^2-b^2}}x=a2−b2​a2​，離心率は a2−b2a\dfrac{\sqrt{a^2-b^2}}{a}aa2−b2​​ になります。詳細は，→離心率の意味と関連する計算
極座標表示極座標で r=l1+εcos⁡θ (l>0,ε>1)r=\dfrac{l}{1+\varepsilon\cos\theta}\:(l>0,\varepsilon>1)r=1+εcosθl​(l>0,ε>1) と表される曲線は楕円です。ε\varepsilonε はさきほど登場した離心率です。lll は半直弦と呼ばれます。
詳細は，→二次曲線（楕円，放物線，双曲線）の極座標表示
円錐曲線楕円は「円錐を母線より急な曲線で切ったときにできる曲線」とみなすこともできます。
詳細は，→二次曲線の分類（四通りの方法）
準円楕円に対して，「その点から楕円に引いた2本の接線が直交する」ような点の集合は円になります。これを楕円の準円と言います。→楕円，放物線，双曲線の準円

発展

発展的なトピックを紹介します。

反射定理

定理

楕円の焦点から出た光は，反射してから反対側の焦点を通る。

→ 楕円の反射定理とその証明

惑星の公転軌道

地球の公転軌道は楕円になります。→地球の公転軌道が楕円であることの導出

楕円積分

$\int_0^{\phi}\sqrt{1-k^2\sin^2\theta}d\theta$ を（第二種）楕円積分といいます。

楕円積分は楕円の弧長の計算に登場します。

計算

楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\:(a>b>0)$ の周の長さを計算する。 $x=a\sin\theta,y=b\cos\theta$ と媒介変数表示すると， $0\leq\theta\leq \phi$ の部分の長さは，

$\begin{aligned} &\int_{0}^{\phi} \sqrt{(a\cos\theta)^2 + (-b\sin\theta)^2} d\theta\\ &= a \int_0^{\phi} \sqrt{(1-\sin^2\theta)+\dfrac{b^2}{a^2} \sin^2\theta} d\theta\\ &= a \int_0^{\phi} \sqrt{1-\dfrac{(a^2-b^2)}{a^2} \sin^2\theta} d \theta \end{aligned}$ である。

周長の計算について，さらに深いトピックは楕円の周の長さの求め方と近似公式をご覧ください。

円は楕円の特殊なケースです。とはいえ，入試ではそのことが本質的に効いてくることはあまりありません。