レムニスケート曲線とその性質
更新
レムニスケート曲線とは,極方程式 で表される曲線である。
しばしば連珠形ということもある。
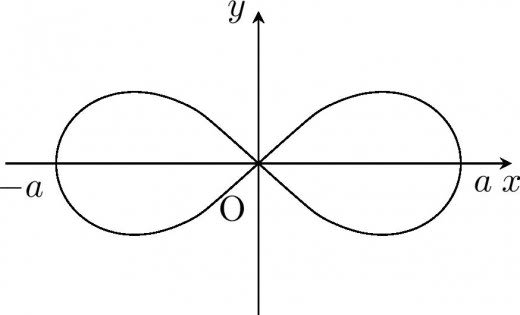
この記事ではレムニスケート(連珠形)の性質とレムニスケート関数・レムニスケート周率について解説します。
レムニスケートは のような形をしたグラフの曲線で,円の変形の一種です。円や三角関数に似た面白い性質があります。
基本的な性質
基本的な性質
直交座標での記述
レムニスケートは, と表すこともできる。
極形式の辺々に を掛けると, である。
面積
レムニスケート の面積 は である。
レムニスケートは原点対称であるため,第1象限の部分の面積を 倍すればよい。。
よって, である。
円との類似性
円との類似性
2点との距離
レムニスケートは円(楕円)の類型です。
楕円は,2つの焦点からの距離の和が一定となるような点の集合から作られる曲線でした。レムニスケートは,その積版になっています。
レムニスケート上の点は, からの距離の積が一定である。
をレムニスケート上の点とする。
からの距離の2乗はそれぞれ である。それらの積を計算すると である。
はレムニスケート上の点であるため, を満たす。
よって,2点からの距離の積は一定値 である。
逆に2点からの距離の積が一定値 であれば,レムニスケートの式が得られます。
2点の距離から定まる曲線群
2点の距離から定まる曲線をまとめておきます。
| 一定であるもの | 名前 |
|---|---|
| 和 | 楕円 |
| 差 | 双曲線 |
| 積 | レムニスケート(カッシーニの卵形線) |
| 商 | アポロ二ウスの円 |
参考記事
レムニスケートの周長
円周率のレムニスケート版を考えます。
レムニスケートの周長の長さと の比をレムニスケート周率といって で表す。
と表される。
円周率とレムニスケート周率の比は具体的に計算することができます。
ただし, は の算術幾何平均である。
詳しい計算は,算術幾何平均とレムニスケートの長さ をどうぞ。
また,レムニスケート周率とレムニスケート関数 もご覧ください。
拡張:カッシーニの卵形線
拡張:カッシーニの卵形線
レムニスケートの拡張にカッシーニの卵形線があります。
カッシーニの卵形線とは, で表される曲線である。
としたらレムニスケートになります。
カッシーニの卵形線上の点は,, からの距離の積が になります。
関連記事
関連記事
レムニスケートのような名前の付けられた特殊な曲線には次のようなものがあります。
-
デカルトの葉線(デカルトの正葉線) → デカルトの葉線の漸近線と面積
-
ニコメデスのコンコイド → ニコメデスのコンコイド
-
パスカルの蝸牛形(リマソン) → パスカルの蝸牛形(リマソン)
-
シッソイド(疾走線) → シッソイド(疾走線)
入試では,ごくごくまれに登場します。











