ニコメデスのコンコイド

レベル: ★ マニアック

更新 2022/10/24

ニコメデスのコンコイド

ニコメデスのコンコイドとは $(x-b)^2 (x^2+y^2) = a^2 x^2$ で表される曲線である。

特殊曲線の1つニコメデスのコンコイドを紹介します。

その他の特殊曲線については媒介変数表示された有名な曲線７つをご覧ください。

コンコイド

極方程式 $r = f(\theta)$ で表される曲線 $C$ と定数 $c$ に対して，極方程式 $r = f(\theta) + c$ で表される曲線をコンコイドといいます。

特に， $C$ として直線 $x = b (r = \dfrac{b}{\cos \theta})$ ， $c = a$ としたものが，ニコメデスのコンコイドとなります。

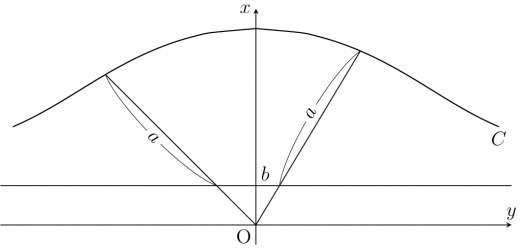
concide_pic

計算

直線 $x=b$ を極方程式で表すと $r = \dfrac{b}{\cos \theta}$ である。

よってニコメデスのコンコイドは $r = a+\dfrac{b}{\cos \theta}$ と表される。

$r = \sqrt{x^2+y^2}$ ， $\cos \theta = \dfrac{x}{r}$ を代入する。

$\sqrt{x^2 + y^2} = a+ \dfrac{b \sqrt{x^2+y^2}}{x}$

変形すると $(x-b) \sqrt{x^2+y^2} = a x$ 辺々二乗して $(x-b)^2 (x^2+y^2) = a^2 x^2$ を得る。

コンコイドの表示をまとめましょう。

コンコイドの表示

コンコイドは直交座標で $(x-b)^2 (x^2+y^2) = a^2 x^2$ 極座標で $r = a + \dfrac{b}{\cos \theta}$ と表される。

角の三等分

「ニコメデスのコンコイドが描ければ」角の三等分をすることができます。
θ\thetaθ を任意にとり，傾き θ\thetaθ の直線上に点 Q(x0,y0)\mathrm{Q} (x_0,y_0)Q(x0​,y0​) を取ります。xxx 軸上（の正の部分）に M\mathrm{M}M を取ります。このとき ∠QOM=θ\angle \mathrm{QOM} = \theta∠QOM=θ です。
a=2OQa = 2\mathrm{OQ}a=2OQ，b=x0b = x_0b=x0​ としたコンコイド CCC を描きます。
y=y0y = y_0y=y0​ と CCC の交点を P\mathrm{P}P とおきます。∠POM=13θ\angle \mathrm{POM} = \dfrac{1}{3} \theta∠POM=31​θ となります。
証明
∠POM=∙\angle \mathrm{POM} = \bullet∠POM=∙ とおく。QP/ ⁣/OM\mathrm{QP} /\!/ \mathrm{OM}QP//OM であるため，錯角は等しく ∠OPQ=∙\angle \mathrm{OPQ} = \bullet∠OPQ=∙ である。
lll と OP\mathrm{OP}OP の交点を R\mathrm{R}R，PR\mathrm{PR}PR の中点を S\mathrm{S}S とおく。
PS=12PR=OQ\mathrm{PS} = \dfrac{1}{2} \mathrm{PR} = \mathrm{OQ}PS=21​PR=OQ である。
加えて QS=PS\mathrm{QS} = \mathrm{PS}QS=PS となる。これより ∠SQP=∙\angle \mathrm{SQP} = \bullet∠SQP=∙ である。
様々な方法で証明ができる。その1つを紹介する。

∠PQR=90∘\angle \mathrm{PQR} = 90^{\circ}∠PQR=90∘ であり，S\mathrm{S}S が PR\mathrm{PR}PR の中点であることから，△PQR\triangle \mathrm{PQR}△PQR の外心は S\mathrm{S}S となる。これより従う。
さらに QS=OQ\mathrm{QS} = \mathrm{OQ}QS=OQ より 
∠QOS=∠QSO=∠SQP+∠SPQ(外角)=∙∙\begin{aligned}
\angle \mathrm{QOS} &= \angle \mathrm{QSO}\\
&= \angle \mathrm{SQP} + \angle \mathrm{SPQ} &(\text{外角})\\
&= \bullet \bullet
\end{aligned}∠QOS​=∠QSO=∠SQP+∠SPQ=∙∙​(外角)​
である。
こうして
θ=∠QOM=∙∙∙
\theta = \angle \mathrm{QOM}
= \bullet \bullet \bullet
θ=∠QOM=∙∙∙
であり，∠POM=13θ\angle \mathrm{POM} = \dfrac{1}{3} \theta∠POM=31​θ である。

その他

入試数学コンテストでコンコイドをテーマとした問題が出題されています。

第2回第4問

$\mathrm{O}$ を原点とする $xy$ 平面を考える。直線 $x = 1$ 上に点 $\mathrm{A}$ を取る。直線 $\mathrm{OA}$ の $x \leqq 0$ の部分に $\mathrm{AB} = 2$ を満たす点 $\mathrm{B}$ が存在するとき, 以下の問いに答えよ。

(1) 直線 $\mathrm{OA}$ と $x$ 軸がなす角を, $x$ 軸の正方向から反時計回りを正として測って $t \, \left( - \dfrac{\pi}{2} \leqq t \leqq \dfrac{\pi}{2} \right)$ とする。 $\mathrm{OB} = r \, (r \geqq 0)$ とするとき, $r$ を $t$ を用いて表せ。

(2) 点 $\mathrm{A}$ が直線 $x = 1$ 上をくまなく動くとき, 点 $\mathrm{B}$ の軌跡を $C$ とする。曲線 $C$ の $y$ 座標の最大値を求めよ。

(3) 曲線 $C$ によって囲まれる領域の面積を求めよ。

→ 入試数学コンテスト第2回第4問解答解説

様々なコンコイド曲線が存在します。角の三等分以外にも $\sqrt[3]{2}$ の作図のために導出されたシッソイドという曲線があります。

レベル: ★ マニアック